
【题目】已知:如图,在菱形ABCD中, BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.
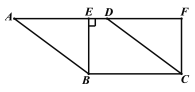
(1)判断四边形EBCF的形状,并证明;
(2)若AF=9,CF=3,求CD的长.
【答案】(1)四边形EBCF是矩形,证明见解析;(2)CD =5
【解析】
(1)由菱形的性质证得EF=BC,由此证明四边形EBCF是平行四边形.,再利用BE⊥AD即可证得四边形EBCF是矩形;
(2)设CD=x,根据菱形的性质及矩形的性质得到DF=9-x,再利用勾股定理求出答案.
(1)四边形EBCF是矩形
证明:∵四边形ABCD菱形,
∴AD=BC,AD∥BC.
又∵DF=AE,
∴DF+DE=AE+DE,
即:EF = AD.
∴ EF = BC.
∴四边形EBCF是平行四边形.
又∵BE⊥AD,
∴ ∠BEF=90°.
∴四边形EBCF是矩形.
(2) ∵ 四边形ABCD菱形,
∴ AD=CD.
∵ 四边形EBCF是矩形,
∴ ∠F=90°.
∵AF=9,CF=3,
∴设CD=x, 则DF=9-x,
∴ ![]() ,
,
解得:![]()
∴CD =5.


科目:初中数学 来源: 题型:
【题目】淘宝网举办“双十一”购物活动许多商家都会利用这个契机进行打折让利的促销活动.
(1)甲网店销售的![]() 商品的成本为30元/件,网上标价为80元/件.“双十一”购物活动当天,甲网店连续两次降价销售
商品的成本为30元/件,网上标价为80元/件.“双十一”购物活动当天,甲网店连续两次降价销售![]() 商品吸引顾客,问该店平均每次降价率为多少时,才能使
商品吸引顾客,问该店平均每次降价率为多少时,才能使![]() 商品的售价为39.2元/件?
商品的售价为39.2元/件?
(2)乙网店销售一批名牌衬衫,平均每天销售20件,每件盈利40元,为了扩大销售,增加盈利减少库存,商场决定采取适当的降价措施,经调查发现,如果每件降价1元,则每天可多售2件.商场若想每天盈利1200元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷每人必选且只选一种,在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了________名学生;在扇形统计图中,表示“![]() ”的扇形所占百分数为__________;
”的扇形所占百分数为__________;
(2)将条形统计图补充完整;
(3)该校共有![]() 名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“![]() ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
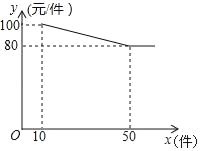
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次涵数![]() 的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数
的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数![]() 的图象.
的图象.
(1)试确定![]() ,
,![]() ,
,![]() 的值;
的值;
(2)指出二次函数![]() 图象的开口方向、对称轴和顶点坐标.
图象的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在直线l上,AD是△ABC的高,∠ABC=45°,BC=6cm,AB=2![]() cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
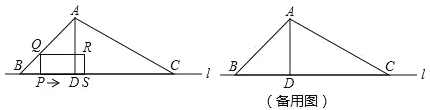
(1)AD= cm;
(2)当点R在边AC上时,求t的值;
(3)求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com