
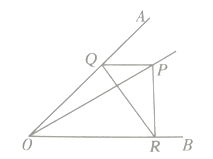
【题目】如图,![]() 是
是![]() 内的一点,
内的一点,![]() ,点
,点![]() 分别在
分别在![]() 的两边上,
的两边上,![]() 周长的最小值是____.
周长的最小值是____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分的学生成绩进行统计,绘制统计图如图(不完整).
类别 | 分数段 |
A | 50.5~60.5 |
B | 60.5~70.5 |
C | 70.5~80.5 |
D | 80.5~90.5 |
E | 90.5~100.5 |
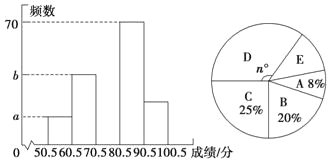
请你根据上面的信息,解答下列问题.
(1)若A组的频数比B组小24,求频数直方图中的a,b的值;
(2)在扇形统计图中,D部分所对的圆心角为n°,求n的值并补全频数直方图;
(3)若成绩在80分以上为优秀,全校共有2 000名学生,估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
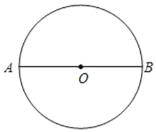
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
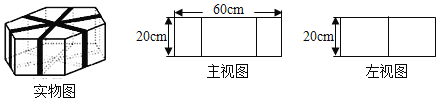
【题目】如图,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图,左视图中包含两个全等的矩形,如果用彩色胶带按如图包扎礼盒,所需胶带长度至少为___________ cm.(精确到0.001 cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中, BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.
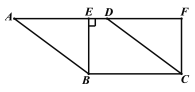
(1)判断四边形EBCF的形状,并证明;
(2)若AF=9,CF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
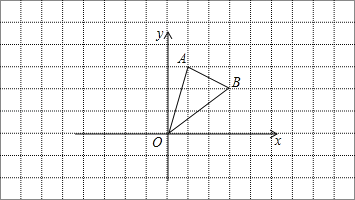
【题目】如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)以原点O为对称中心,画出△ AOB与关于原点对称的△ A2 O B2;
(4)以原点O为旋转中心,画出把△AOB顺时针旋转90°的图形△A3 O B3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com