
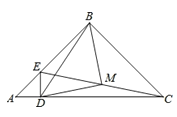
【题目】已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.
(1)求证:△BMD为等腰直角三角形;
(2)当点E运动多少秒时,△BMD的面积为12.5cm2?
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得BM=![]() CE,DM=
CE,DM=![]()
CE,得出BM=DM,再由等腰三角形的性质和三角形的外角性质证出∠BMD=90°即可;
(2)由等腰直角三角形的面积求出BM,得出CE,由勾股定理求出BE,得出AE,即可得出结果.
试题解析:(1)∵∠ABC=90°,DE⊥AC,点M为EC的中点,AB=BC,
∴BM=![]() CE=CM,DM=
CE=CM,DM=![]() CE=CM,∠BAC=∠ACB=45°,
CE=CM,∠BAC=∠ACB=45°,
∴BM=DM,∠MBC=∠MCB,∠MDC=∠MCD,
∵∠BME=∠MBC+∠MCB,∠DME=∠MDC+∠MCD,∠MCB+∠MCD=∠ACB=45°,
∴∠BMD=∠BME+∠DME=45°+45°=90°,
∴△BMD为等腰直角三角形;
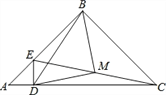
(2)由(1)得:△BMD为等腰直角三角形,
∴△BMD的面积=![]() BMDM=
BMDM= ![]() BM2=12.5,解得:BM=5,
BM2=12.5,解得:BM=5,
∴CE=2BM=10cm,由勾股定理得:BE= ![]() =6(cm),
=6(cm),
∴AE=AB﹣BE=2cm,∴2÷1=2(s),
即当点E运动2秒时,△BMD的面积为12.5cm2.


科目:初中数学 来源: 题型:
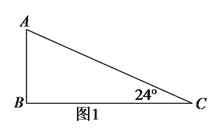
【题目】(![]() )如图
)如图![]() 中,
中,![]() ,请用直尺和圆规作一条直线,把
,请用直尺和圆规作一条直线,把![]() 分割成两个等腰三角形(不写作法,但须保留作图痕迹).
分割成两个等腰三角形(不写作法,但须保留作图痕迹).
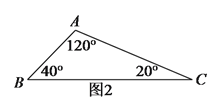
(![]() )如图
)如图![]() 中,
中,![]() 的三个内角分别为
的三个内角分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,在
,在![]() 上找一个点
上找一个点![]() ,使
,使![]() 为等腰三角形,求出
为等腰三角形,求出![]() 的长(可用含
的长(可用含![]() 的代数式表示).
的代数式表示).


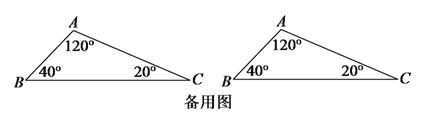
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x、y是有理数,设N=3x2+2y2﹣18x+8y+35,则N( )
A. 一定是负数 B. 一定不是负数 C. 一定是正数 D. N的取值与x、y的取值有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是:将ΔBCD绕点D逆时针旋转90°到ΔAED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且ΔCDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.




图① 图② 图③ 图④
简单应用:
(1)在图①中,若AC=![]() ,BC=2
,BC=2![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
拓展延伸:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知⊙O上依次有A、B、C、D四个点,![]() =
=![]() ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
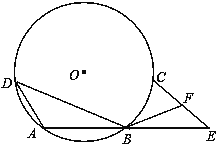
(1)求证:BF=![]() BD;
BD;
(2)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com