
【题目】如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,![]() ≈1.7).
≈1.7).

【答案】大树CD的高度约为6.6米.
【解析】
作BF⊥AE于F,则FE=BD=6.4米,DE=BF,设BF=x米,则AF=AF=![]() x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=8米,AF≈13.6米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=8米,AF≈13.6米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
作BF⊥AE于F,如图所示:
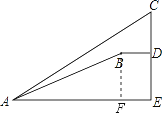
则FE=BD=6.4米,DE=BF,
∵斜坡AB的坡角为30°,
∴AF=![]() BF,
BF,
设BF=x米,则AF=![]() x米,
x米,
在Rt△ABF中,由勾股定理得:x2+(![]() x)2=162 ,
x)2=162 ,
解得:x=8,
∴DE=BF=8米,AF≈13.6米,
∴AE=AF+FE=20米,
在Rt△ACE中,CE=AEtan36°≈20×0.73=14.6米,
∴CD=CE﹣DE=14.6﹣8=6.6米.
故大树CD的高度约为6.6米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
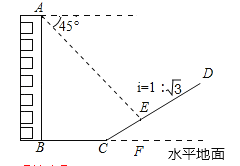
【题目】(8分)如图,一楼房AB后有一假山,其坡度为![]() ,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测的假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
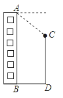
【题目】如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为________m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋子中装有3个带号码的球,球号分别是2,3,5,这些球除号码不同外其他均相同.
(1)从袋中随机摸出一个球,求恰好是3号球的概率;
(2)从袋中随机摸出一个球,再从剩下的球中随机摸出一个球,用树形图列出所有可能出现的结果,并求两次摸出球的号码之和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
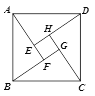
【题目】如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中四个直角三角形是全等的,若大正方形ABCD的面积是小正方形EFGH面积的13倍,则![]() 的值为______________.
的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学上学期全部参加了捐款活动,捐款情况如下统计表:
金额(元) | 5 | 10 | 15 | 20 | 25 | 30 |
人数(人) | 8 | 12 | 10 | 6 | 2 | 2 |
(1)求该班学生捐款额的平均数和中位数;
(2)试问捐款额多于15元的学生数是全班人数的百分之几?
(3)已知这笔捐款是按3:5:4的比例分别捐给灾区民众、重病学生、孤老病者三种被资助的对象,问该班捐给重病学生是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
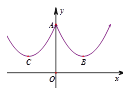
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
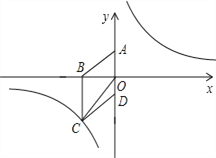
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且![]() (0,3)、
(0,3)、![]() (﹣4,0).
(﹣4,0).
(1)求经过点![]() 的反比例函数的解析式;
的反比例函数的解析式;
(2)设![]() 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以![]() 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com