
����Ŀ���Ķ�������ϣ�
��ѧϰ��Բ����һ��ʱ����ʦ��ͬѧ�Dz�����һ���߹���ͼ�⣺
�߹���ͼ����Բ��һ����Բ�����ߡ�
��֪��PΪ��O��һ�㡣
������������P�ġ�O������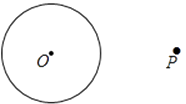
С�����������£�
��ͼ��
������OP�����߶�OP�Ĵ�ֱƽ����MN��OP��C
���Ե�CΪԲ�ģ�CO�ij�Ϊ�뾶��Բ������O ��A��B����
����ֱ��PA��PB����ֱ��PA��PB�������������
��ʦ��ΪС����������ȷ��
��ش�����OA��OB��֤��OAP=��OBP=90�㣬�����������ɴ˿�֤��ֱ��PA��PB���ǡ�O�����ߣ��������� ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ������Բ���Σ����Ŀ��ABΪ60�ף�����PMΪ18�ף�����ˮ���ĵ����ֻ��30��ʱ����Ҫ��ȡ������ʩ����������ˮ��ֻ��4�ף���PN=4��ʱ���Ƿ��ȡ������ʩ���� ![]() =1.414��
=1.414�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
��ͼ1����ƽ��ֱ������ϵxOy�У�A��B���������ֱ�ΪA��x1 �� y1����B��x2 �� y2�����ɹ��ɶ�����AB2=|x2��x1|2+|y2��y1|2 �� ����A��B�����ľ���ΪAB= ![]() ��
��
����֪����Բ���Կ��ɵ�Բ�ĵľ�����ڰ뾶�ĵ�ļ��ϣ���ͼ2����ƽ��ֱ������ϵxOy�У�A ��x��y��ΪԲ������һ�㣬���A��ԭ��ľ����ƽ��ΪOA2=|x��0|2+|y��0|2 �� ����O�İ뾶OAΪrʱ����O�ķ��̿�дΪ��x2+y2=r2 ��
������չ��
���Բ������ΪP ��a��b�����뾶Ϊr����ô��P�ķ��̿���дΪ����x��a��2+��y��b��2=r2�� ��
�ۺ�Ӧ�ã�
��ͼ3����P��x��������ԭ��O��P������Ϊ��0��6����A�ǡ�P��һ�㣬����OA��ʹ��POA=30�㣬��PD��OA������ΪD���ӳ�PD��x���ڵ�B������AB��
��֤��AB�ǡ�P�����ߣ�
���Ƿ���ڵ��ĵ�O��P��A��B���붼��ȵĵ�Q�������ڣ���Q�����꣬��д���Ե�QΪԲ�ģ�OQ��Ϊ�뾶�ġ�Q�ķ��̣��������ڣ�˵�����ɣ�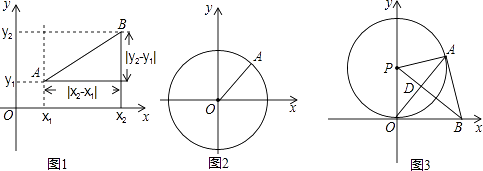
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=��2x2+��m+9��x��6�ĶԳ�����x=2��
��1���������߱���ʽ�Ͷ������ꣻ
��2����������������ƽ��1����λ��ƽ�ƺ����������ԭ�������ཻ�ڵ�A�����A�����ꣻ
��3��������y=��2x2+��m+9��x��6��y�ύ�ڵ�C����A����ƽ�ƺ������ߵĶԳ���ĶԳƵ�Ϊ��B�������������ڵ�A��C�͵�A��B֮��IJ��֣�������A��B��C�� ��Ϊͼ��M����ֱ��y=2x��2����ƽ��b��b��0������λ����ƽ�ƹ�����ֱ����ͼ��Mʼ�������������㣬����д��b��ȡֵ��Χ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ�༶������һ���������Ƚ��Ľ�Ʒ����֪һ�Ƚ���Ʒ6Ԫ�����Ƚ���Ʒ4Ԫ�����Ƚ���Ʒ2Ԫ�����л������ķ��������ͼ����С�չ���Ʒ���õ�ƽ�����������ֱ�Ϊ��������%

A. 2Ԫ��3Ԫ B. 2.5Ԫ��2.5Ԫ C. 3Ԫ��2Ԫ D. 3Ԫ��3Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��ѧϰ��Բ����һ��ʱ����ʦ��ͬѧ�Dz�����һ���߹���ͼ�⣺
�߹���ͼ����Բ��һ����Բ�����ߡ�
��֪��PΪ��O��һ�㡣
������������P�ġ�O������
С�����������£�
��ͼ��
������OP�����߶�OP�Ĵ�ֱƽ����MN��OP��C
���Ե�CΪԲ�ģ�CO�ij�Ϊ�뾶��Բ������O ��A��B����
����ֱ��PA��PB����ֱ��PA��PB�������������
��ʦ��ΪС����������ȷ��
��ش�����OA��OB��֤��OAP=��OBP=90�㣬�����������ɴ˿�֤��ֱ��PA��PB���ǡ�O�����ߣ��������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��F�ֱ��ڱ�AB��CD�ϣ�EF��BC��AE��BE=1��2���Խ���AC��EF��G����BC=10cm��AD=6cm����EF�ij�����______ cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ΪӦ��Խ��Խ���ص���������������ͬѧ���ڰ༶�ļҳ�ίԱ�ᣬ��Ϊ�ð༯�ʾ���һ̨���͵Ŀ�������������֪��ij�̳������ͺŵĿ�������������۵İ��۳��ۣ�ÿ̨�����������Կɻ���![]() ����֪���ͺſ����������Ľ���Ϊ
����֪���ͺſ����������Ľ���Ϊ![]() Ԫ��
Ԫ��
![]() ��ÿ����������ı�ۣ�
��ÿ����������ı�ۣ�
![]() ����
���ð���![]() ��ѧ������ð�ÿλѧ���ҳ�Ӧƽ����������Ԫ��
��ѧ������ð�ÿλѧ���ҳ�Ӧƽ����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��ͼ1����ƽ��ֱ������ϵxOy�У�ֱ��y1=ax+b��˫����y2= ![]() ����A��1��3����B����3����1�����㣮
����A��1��3����B����3����1�����㣮
�۲�ͼ���֪��
�ٵ�x=��3��1ʱ��y1=y2��
�ڵ���3��x��0��x��1ʱ��y1��y2 �� ��ͨ���۲캯����ͼ���Եõ�����ʽax+b�� ![]() �Ľ⼯��
�Ľ⼯��
������һ�����⣺��ʽx3+4x2��x��4��0�Ľ⼯��
ijͬѧ����ѧϰ����֪ʶ�ľ��飬����ʽx3+4x2��x��4��0�Ľ⼯������̽����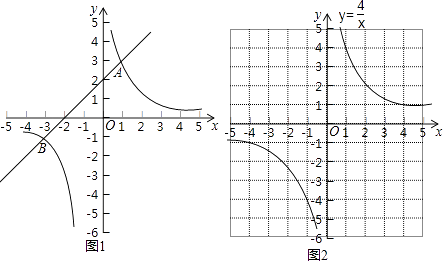
����������̽�����̣��뽫��2������3������4������������
��1��������ʽ����������ת����
��2�����캯��������ͼ��
��y3=x2+4x��1��y4= ![]() ����ͬһ����ϵ�зֱ�������������ͼ��
����ͬһ����ϵ�зֱ�������������ͼ��
˫����y4= ![]() ��ͼ2��ʾ�����ڴ�����ϵ�л���������y3=x2+4x��1���������б���
��ͼ2��ʾ�����ڴ�����ϵ�л���������y3=x2+4x��1���������б���
��3��ȷ����������ͼ����ĺ����꣬�۲���������������ͼ���벢ͨ�����뺯������ʽ��֤��֪������y3=y4������x��ֵΪ
��4������ͼ��д���⼯
��ϣ�1�������۽�����۲�����������ͼ���֪������ʽx3+4x2��x��4��0�Ľ⼯
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com