
【题目】如图1,点P为四边形ABCD所在平面上的点,如果∠PAD=∠PBC,则称点P为四边形ABCD关于A、B的等角点,以点C为坐标原点,BC所在直线为![]() 轴建立平面直角坐标系,点B的横坐标为﹣6.
轴建立平面直角坐标系,点B的横坐标为﹣6.
(1)如图2,若A、D两点的坐标分别为A(﹣6,4)、D(0,4),点P在DC边上,且点P为四边形ABCD关于A、B的等角点,则点P的坐标为 _________ ;
(2)如图3,若A、D两点的坐标分别为A(﹣2,4)、D(0,4).
①若P在DC边上时,则四边形ABCD关于A、B的等角点P的坐标为 _________ ;
②在①的条件下,将PB沿![]() 轴向右平移
轴向右平移![]() 个单位长度(0<
个单位长度(0<![]() <6)得到线段P′B′,连接P′D,B′D,试用含
<6)得到线段P′B′,连接P′D,B′D,试用含![]() 的式子表示P′D2+B′D2,并求出使P′D2+B′D2取得最小值时点P′的坐标;
的式子表示P′D2+B′D2,并求出使P′D2+B′D2取得最小值时点P′的坐标;
③如图4,若点P为四边形ABCD关于A、B的等角点,且点P坐标为(1, ![]() ),求
),求![]() 的值;
的值;
④以四边形ABCD的一边为边画四边形,所画的四边形与四边形ABCD有公共部分,若在所画的四边形内存在一点P,使点P分别是各相邻两顶点的等角点,且四对等角都相等,请直接写出所有满足条件的点P的坐标.
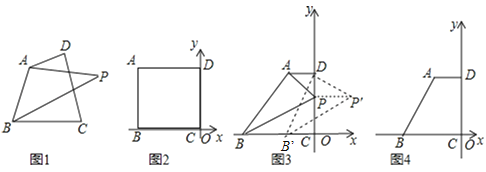
【答案】(1)(0,2);(2)①(0,3);②2m2-12m+53,(3,3);③2.8;④(-1,3),(-2,2),(-3,3),(-2,0)
【解析】试题分析:(1)连结AP,BP,由全等三角形的性质就可以得出PD=PC而得出结论;
(2)①由△ADP∽△BCP就可以得出![]() 而求出结论;
而求出结论;
②求出代表P′D2+B′D2的方程式,并求最小值.
③画图求证△PAM∽△PBN,值得注意的是本题有两个图形,容易漏掉一个答案.
④由题意可知,必须是正方形才能满足题干要求.
试题解析:解:(1)由B点坐标(﹣6,0),A点坐标(﹣6,4)、D点坐标(0,4),可以得出四边形ABCD为矩形,
∵P在CD边上,且∠PAD=∠PBC,∠ADP=∠BCP,BC=AD;
∴△ADP≌△BCP,∴CP=DP,
∴P点坐标为(0,2);
(2)①∵∠DAP=∠CBP,∠BCP=∠ADP=90°,
∴△ADP∽△BCP,
∴![]() =
=![]() =
=![]() ,
,
∴CP=3DP,∴CP=3,DP=1,
∴P点坐标为(0,3);
②如图3,由题意,易得 B′(m﹣6,0),P′(m,3)
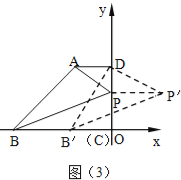
由勾股定理得P′D2+B′D2=PP′2+PD2+OD2+B′C2=m2+(4﹣3)2+42+(m﹣6)2=2m2﹣12m+53,
∵2>0
∴P′D2+B′D2有最小值,
当m=﹣![]() =3时,(在0<m<6范围内)时,P′D2+B′D2有最小值,此时P′坐标为(3,3);
=3时,(在0<m<6范围内)时,P′D2+B′D2有最小值,此时P′坐标为(3,3);
③由题意知,点P在直线x=1上,延长AD交直线x=1于M,
(a)如图,当点P在线段MN上时,易证△PAM∽△PBN,

∴![]() ,
,
即![]() ,
,
解得t=2.8
(b)如图,当点P为BA的延长线与直线x=1的交点时,易证△PAM∽△PBN,
∴![]() ,即
,即![]() ,解得t=7,
,解得t=7,
综上可得,t=2.8或t=7;
④因满足题设条件的四边形是正方形,
故所求P的坐标为(﹣1,3),(﹣2,2),(﹣3,3),(﹣2,0).


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )

A. 3 B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的裁剪线,并直接写出每种不同分割后得到的最小等腰直角三角形面积.(注:不同的分法,面积可以相等).

(1)________;(2)________;(3)________;(4)________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB= 90°,CD是∠ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E ,O,F.求证:四边形CEDF是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com