练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

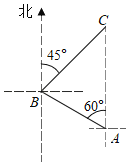
    【题目】科技改变生活，手机导航极大方便了人们的出行，如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60方向行驶8千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地的距离．（结果保留根号）

    【答案】4千米

    【解析】

    过B作BD⊥AC于点D，在直角△ABD中利用三角函数求得BD的长，然后在直角△BCD中利用三角函数求得BC的长．

    解：过B作BD⊥AC于点D．

    在Rt△ABD中，BD＝ABsin∠BAD＝8×＝4（千米），

    ∵△BCD中，∠CBD＝45°，

    ∴△BCD是等腰直角三角形，

    ∴CD＝BD＝4（千米），

    ∴BC＝BD＝4（千米）．

    答：B，C两地的距离是4千米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】初三（1）班针对“垃圾分类”知晓情况对全班学生进行专题调查活动，对“垃圾分类”的知晓情况分为、、、四类．其中，类表示“非常了解”，类表示“比较了解”，类表示“基本了解”，类表示“不太了解”，每名学生可根据自己的情况任选其中一类，班长根据调查结果进行了统计，并绘制成了不完整的条形统计图和扇形统计图．

    “垃圾分类”知晓情况各类别人数条形统计图 “垃圾分类”知晓情况各类别人数扇形统计图

    根据以上信息解决下列问题：

    （1）初三（1）班参加这次调查的学生有______人，扇形统计图中类别所对应扇形的圆心角度数为______°；

    （2）求出类别的学生数，并补全条形统计图；

    （3）类别的4名学生中有2名男生和2名女生，现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

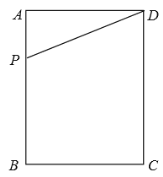
    【题目】如图，在矩形ABCD中，AB=4，BC=3，点P是边AB上的一动点，连接DP，

    （1）若将△DAP沿DP折叠，点A落在矩形的对角线上点A处，试求AP的长；

    （2）点P运动到某一时刻，过点P作直线PE交BC于点E，将△DAP与△PBE分别沿DP与PE折叠，点A与点B分别落在点A，B处，若P，A，B三点恰好在同一直线上，且AB=2，试求此时AP的长．

    （3）当点P运动到边AB的中点处时，过点P作直线PG交BC于点G，将△DAP与△PBG分别沿DP与PG折叠，点A与点B重合于点F处，请直接写出F到BC的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某校九年级男生的体能情况，体育老师从中随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制成尚不完整的扇形图和条形图，根据图形信息回答下列问题：

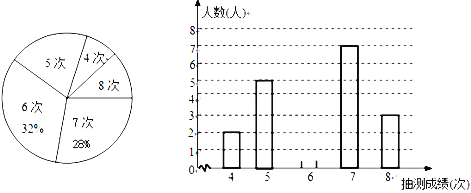
    （1）本次抽测的男生有________人，抽测成绩的众数是_________；

    （2）请将条形图补充完整；

    （3）若规定引体向上6次以上（含6次）为体能达标，则该校125名九年级男生中估计有多少人体能达标？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列等式：

    第一个等式：；

    第二个等式：；

    第三个等式：；

    第四个等式：；

    按上述规律，回答下列问题：

    （1）请写出第六个等式：a6= = ；

    （2）用含n的代数式表示第n个等式：an= = ；

    （3）a1+a2+a3+a4+a5+a6= （得出最简结果）；

    （4）计算：a1+a2+…+an．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过边长为3的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：有一个内角为90°，且对角线相等的四边形称为准矩形．

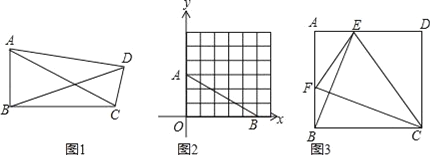
    （1）①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=　 　；

    ②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是　 　；（整点指横坐标、纵坐标都为整数的点）

    （2）如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；

    （3）已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列判断正确的是（ ）．

    A.数据3，5，4，1，-2的中位数为4

    B.从初三月考成绩中抽取100名学生的数学成绩，这100名学生是总体的一个样本

    C.甲、乙两人各射靶5次，已知方差，，那么乙的射击成绩较稳定

    D.了解云南省昆明市居民疫情期间的出行方式，采用全面调查的方式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

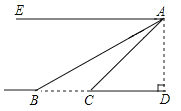
    【题目】如图，为测量某条河的宽度BC，工程队用无人机在距地面高度为200米的A处测得B，C两点的俯角分别为30°和45°，且点B，C，D在同一水平直线上，求A，C之间的距离和这条河的宽度BC．（结果保留根号）

    查看答案和解析>>

    同步练习册答案