
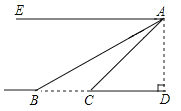
【题目】如图,为测量某条河的宽度BC,工程队用无人机在距地面高度为200米的A处测得B,C两点的俯角分别为30°和45°,且点B,C,D在同一水平直线上,求A,C之间的距离和这条河的宽度BC.(结果保留根号)
科目:初中数学 来源: 题型:
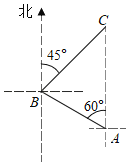
【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60方向行驶8千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点![]() ,有下列结论:
,有下列结论:
①abc![]() 0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c
0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c![]() 0; ⑤a﹣b≥m(am﹣b);
0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是______.(填写正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
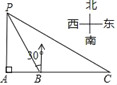
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点
的图像交于两点![]() ,
,![]() .
.
(1)求反比例函数与一次函数的函数表达式;
(2)在反比例函数的图像上找点![]() ,使得点
,使得点![]() 构成以
构成以![]() 为底的等腰三角形,请求出所有满足条件的点
为底的等腰三角形,请求出所有满足条件的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
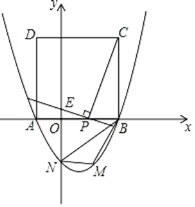
【题目】如图,抛物线y=x2+bx+c与x轴的交点为A(﹣1,0),B(3,0),与y轴交于点N,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接CP、DP,过点P作CP的垂线与y轴交于点E.
(1)求该抛物线的函数关系表达式;
(2)当CP+DP的值最小时,求E点的坐标;
(3)在第四象限的抛物线上任取一点M,连接MN、MB,是否存在点M使得△MNB为直角三角形;若存在,求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
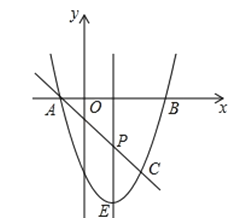
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1,0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)求抛物线的函数解析式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com