
【题目】(1)解下列方程:①x2﹣2x﹣2=0;②2x2+3x﹣1=0;③2x2﹣4x+1=0;④x2+6x+3=0;
(2)上面的四个方程中,有三个方程的一次项系数有共同特点,请你用代数式表示这个特点,并推导出具有这个特点的一元二次方程的求根公式_______.
【答案】![]()
【解析】
(1)直接代入公式计算即可.
(2)其中方程①③④的一次项系数为偶数2n(n是整数).然后再利用求根公式代入计算即可.
(1)①解方程x2-2x-2=0①,
∵a=1,b=-2,c=-2,
∴x=![]() =
=![]() ,
,
∴x1=1+![]() ,x2=1
,x2=1![]() .
.
②解方程2x2+3x-l=0,
∵a=2,b=3,c=-1,
∴x=![]() =
=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() .
.
∴x1=![]() ,x2=
,x2=![]()
③解方程2x2-4x+1=0,
∵a=2,b=-4,c=1,
∴x=![]() =
=![]() ,
,
x1=![]() ,x2=
,x2=![]() .
.
④解方程x2+6x+3=0,
∵a=1,b=6,c=3,
∴x=![]() =
=![]() =
=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() .
.
(2)其中方程①③④的一次项系数为偶数2n(n是整数).
一元二次方程ax2+bx+c=0,其中b2-4ac≥0,b=2n,n为整数.
∵b2-4ac≥0,即(2n)2-4ac≥0,
∴n2-ac≥0,
∴x=![]() =
=![]() =
=![]() =
=![]()
∴一元二次方程ax2+2nx+c=0(n2-ac≥0)的求根公式为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将任意两点P(x1,y1)与Q(x2,y2)之间的“直距”定义为:DPQ=|x1﹣x2|+|y1﹣y2|.
例如:点M(1,﹣2),点N(3,﹣5),则DMN=|1﹣3|+|﹣2﹣(﹣5)|=5.已知点A(1,0)、点B(﹣1,4).
(1)则DAO= ,DBO= ;
(2)如果直线AB上存在点C,使得DCO为2,请你求出点C的坐标;
(3)如果⊙B的半径为3,点E为⊙B上一点,请你直接写出DEO的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内有一等腰Rt△ABC,∠ACB=90°,点A在直线l上.过点C作CE⊥1于点E,过点B作BF⊥l于点F,测量得CE=3,BF=2,则AF的长为( )

A. 5 B. 4 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
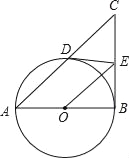
【题目】如图,在⊙O中,C,D分别为半径OB,弦AB的中点,连接CD并延长,交过点A的切线于点E.
(1)求证:AE⊥CE.
(2)若AE=![]() ,sin∠ADE=
,sin∠ADE=![]() ,求⊙O半径的长.
,求⊙O半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
(1)证明OE∥AD;
(2)①当∠BAC= °时,四边形ODEB是正方形.
②当∠BAC= °时,AD=3DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成。为了种植“花海”,需要从甲乙两地向大圩A.B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A.B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
(1)设甲地运往![]() 棚营养土
棚营养土![]() 吨,请用关于
吨,请用关于![]() 的代数式完成下表;
的代数式完成下表;
运往A.B两地的吨数 | ||
A | B | |
甲地 |
|
|
乙地 | ___ | ___ |
(2)设甲地运往A棚营养土![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式(要求写出自变量取值范围).
(吨)的函数关系式(要求写出自变量取值范围).
(3)当甲、乙两地各运往A.B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com