
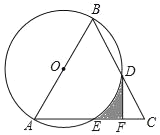
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC,AC于点D,E,过点D作DF⊥AC于点F
(1)求证:DF是⊙O的切线;
(2)若∠C=60°,⊙O的半径为2,求由弧DE,线段DF,EF围成的阴影部分的面积(结果保留根号和π)
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接AD、OD,先利用等腰三角形的性质证CD=BD,再证OD为△ABC的中位线得DO∥AC,根据DF⊥AC可得;
(2)连接OE、BE,DE,根据已知条件得到△ABC是等边三角形,求得DE∥AB,于是得到S△ADE=S△ODE,根据阴影部分面积=S梯形EFDO-S扇形DOE计算可得.
解:(1)如图,连接AD、OD,
∵AB为⊙O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
∵OA=OB,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,BE,DE,
∵AB=AC,∠C=60°,
∴△ABC是等边三角形,
∵AB为⊙O的直径,
∴BE⊥AC,
∴AE=CE,
∴DE∥AB,
∴S△ADE=S△ODE,
∵⊙O的半径为2,∠BAD=∠CAD=30°,
∴AD=2![]() ,
,
∴DF=![]() AD=
AD=![]() ,AF=3,
,AF=3,
∵∠DOE=2∠DAC=60°,
∴阴影部分面积为S梯形EFDO﹣S扇形DOE
=S三角形ADF﹣S扇形DOE=![]() ×
×![]() ×3﹣
×3﹣![]() =
=![]() ﹣
﹣![]() .
.
故答案为(1)证明见解析;(2)![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】南岸区近年修建和完善了不少道路,其中一段道路两侧的绿化任务计划由甲、乙、丙、丁四个人完成.道路两侧的植树数量相同,如果乙、丙、丁同时开始植树,丁在道路左侧,乙和丙在道路右侧,2小时后,甲加入,在道路左侧与丁一起植树.这样恰好能保证道路两侧的植树任务同时完成.已知甲、乙、丙、丁每小时能完成的植树数量分别为6、7、8、10棵.实际在植树时,四人一起开始植树,甲和丁在道路左侧、乙和丙在道路右侧,为保证右侧比左侧提前5小时完成植树任务,甲中途转到右侧与乙和丙一起按要求完成了任务,左侧剩下的任务由丁独自完成、则在本次植树任务中,甲比丁少植树_____棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
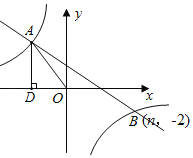
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先测量出窗口A到地面的距离AB=16m,又测得从A处看建筑物底部C的俯角为![]() =30°,看建筑物顶部D的仰角为
=30°,看建筑物顶部D的仰角为![]() =45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.
=45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.
(1)求AB与CD之间的距离(结果保留根号);
(2)求建筑物CD的高度(结果精确到0.1m).(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间(用t表示,单位:小时),采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如下图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如下图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
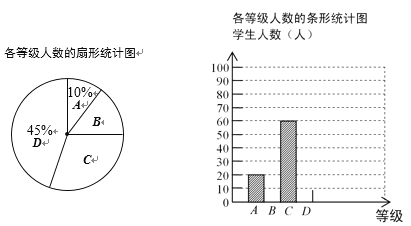
(1)求本次调查的学生人数;
(2)求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
(3)若该校共有学生1200人,试估计每周课外阅读时间不少于3小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年初,新型冠状病毒肺炎侵袭湖北,武汉是重灾区,某爱心人士两次购买N95口罩支援武汉,第一次花了500000元,第二次花了770000,购买了同样的N95口罩,已知第二次购买的口罩的单价是第一次的1.4倍,且比第一次多购进了10000个,求该爱心人士第一次购进口罩的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一文具厂接到生产一批橡皮和水笔的任务,已知该文具厂销售200个橡皮和200个水笔的利润为160元,销售100个橡皮和200个水笔的利润为130元.已知该文具厂每天生产橡皮和水笔共4500个,生产橡皮和水笔每个成本分别为2元,3元,设每天生产橡皮![]() 个,该文具厂每天生产成本为
个,该文具厂每天生产成本为![]() 元.
元.
(1)求橡皮和水笔的销售单价;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若该文具厂每天最多投入成本为10000元,求该文具厂每天获得利润最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
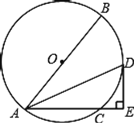
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AE=![]() ,求AC长.
,求AC长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com