
【题目】如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.

(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB正确的关系式.
【答案】(1)见解析;(2)BE=EF,理由见解析;(3)小李的发现是正确的,理由见解析
【解析】
(1)如图1,连接AP,由BC是半⊙O的直径,AD⊥BC于D,得到∠ACB+∠ABC=∠BAD+∠ABD=90°,于是得到∠ACB=∠BAD,根据圆周角定理得到∠P=∠ACB=∠ABP,即可求出结论;
(2)根据圆周角定理求出∠ABE=∠BAE,求出AE=BE,求出∠CAD=∠AFB,求出AE=EF,即可得出答案;
(3)根据全等三角形的性质和判定求出BG=CF,AB=AG,即可得出答案.
(1)如图1,连接AP,
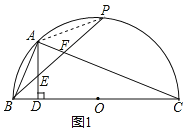
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE;
(2)BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF;
(3)小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
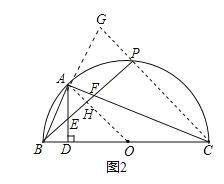
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
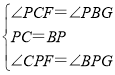 ,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
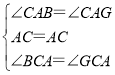
∴△BAC≌△GAC(ASA),
∴AG=AB=![]() BG,
BG,
∴CF=2AB.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
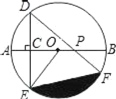
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2![]() ,∠DPA=45°.则图中阴影部分的面积为____.
,∠DPA=45°.则图中阴影部分的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b-a>c:③4a+2b+c>0;④3a>-c;⑤a+b>m(am+b)(m≠1的实数).其中结论正确的有( )
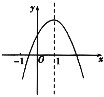
A. ①②③
B. ②③⑤
C. ②③④
D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象与函数
的图象与函数![]() (
(![]() )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).

(1)求函数![]() 的表达式和点B的坐标;
的表达式和点B的坐标;
(2)观察图象,比较当x>0时![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每位同学都能感受到日出时美丽的景色.下图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
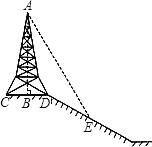
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=20m,DE=30m,小明和小华的身高都是1.5m,同一时刻,小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
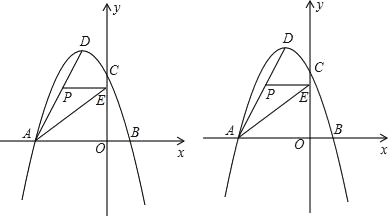
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
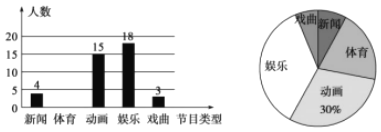
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com