
【题目】已知:关于x的方程![]() 有实数根.
有实数根.
(1)求m的取值范围;
(2)若方程的根为有理数,求正整数m的值.
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4与二次函数y=ax2+c的图像的一个交点坐标为(1,2),另一个交点是该二次函数图像的顶点
(1)求k,a,c的值;
(2)过点A(0,m)(0<m<4)且垂直于y轴的直线与二次函数y=ax2+c的图像相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
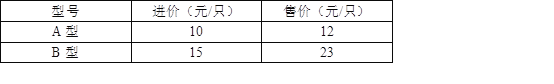
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,点A(-1,2)在函数![]() (x<0)的图象上.
(x<0)的图象上.
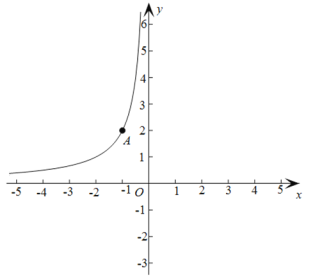
(1)求m的值;
(2)过点A作y轴的平行线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点B,与函数
交于点B,与函数![]() (x<0)的图象交于点C,与
(x<0)的图象交于点C,与![]() 轴交于点D.
轴交于点D.
①当点C是线段BD的中点时,求b的值;
②当BC<BD时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
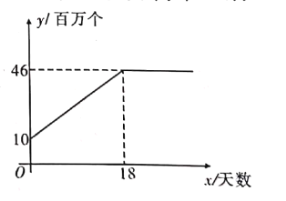
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
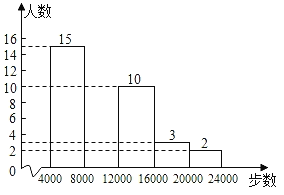
【题目】现如今”微信运动“被越来越多的人关注和喜爱,某数学兴趣小组随机调查了该校50名教师某日“微信运动“中的行走步数情况,并将统计的数据绘制成了如下两幅不完整的统计图表.请根据以上信息,解答下列问题:
(1)求出a,b,c,d的值,并补全频数分布直方图.
(2)本市约有58000名教师,用调查的样本数据估计日行步数超过12000步(包含12000步)的教师有多少名?
(3)若在被调查的50名教师中.选取日行步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师的日行走步数恰好都在20000步(包含20000步)以上的概率.
步数(x) | 频数 | 频率 |
0≤x<4000 | a | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | b | 0.24 |
12000≤x<16000 | 10 | c |
16000≤x<20000 | 3 | 0.06 |
2000≤x<24000 | 2 | d |
查看答案和解析>>
科目:初中数学 来源: 题型:
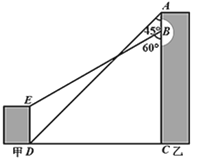
【题目】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:![]() ,
,![]() ,精确到0.1m.)
,精确到0.1m.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过点B(1,0)的抛物线![]() 与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
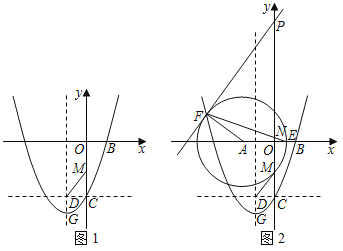
(1)求抛物线的表达式;
(2)求![]() 的最小值以及相应的点M的坐标;
的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com