
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)填空:∠CAM=__________度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.



【答案】30;
【解析】(1)根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE而有∠CBE=∠CAD=30°而得出结论;当点D在线段MA的延长线上时,如图3,通过得出△ACD≌△BCE同样可以得出结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=60°.
∵线段AM为BC边上的中线
∴∠CAM=![]() ∠BAC,
∠BAC,
∴∠CAM=30°.
故答案为:30;
(2)∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACD+∠DCB=∠DCB+∠BCE
∴∠ACD=∠BCE.
在△ADC和△BEC中,AC=BC,∠ACD=∠BCE,CD=CE,,
∴△ACD≌△BCE(SAS);
(3)∠AOB是定值,∠AOB=60°,
理由如下:
①当点D在线段AM上时,如图1,

由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,
又∠ABC=60°
∴∠CBE+∠ABC=60°+30°=90°,
∵△ABC是等边三角形,线段AM为BC边上的中线
∴AM平分∠BAC,即∠BAM=![]() ∠BAC=
∠BAC=![]() ×60°=30°
×60°=30°
∴∠BOA=90°-30°=60°.
②当点D在线段AM的延长线上时,如图2,
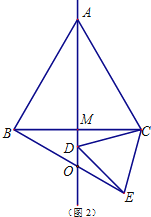
∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACB+∠DCB=∠DCB+∠DCE
∴∠ACD=∠BCE
在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD=30°,
同理可得:∠BAM=30°,
∴∠BOA=90°-30°=60°.
③当点D在线段MA的延长线上时,如图3,
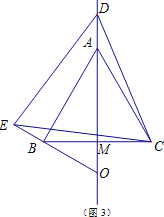
∵△ABC与△DEC都是等边三角形
∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACD+∠ACE=∠BCE+∠ACE=60°
∴∠ACD=∠BCE
在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠CBE=∠CAD
同理可得:∠CAM=30°
∴∠CBE=∠CAD=150°
∴∠CBO=30°,∠BAM=30°,
∴∠BOA=90°-30°=60°.
综上,当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.
“点睛”边三角形的性质的运用,直角三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.


科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为__________;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)
(1)求出两个动点运动的速度;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;
(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人在原地休息。已知甲先出发2秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,下列结论中正确的有几个?(1)甲速为每秒4米;(2)乙速为每秒5米;(3)a=8;(4)b=100;(5)c=125 ( )
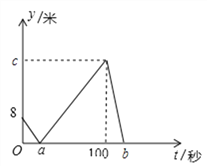
A. 4个 B. 2个 C. 3个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016宁夏第4题)为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )

A.2和1 B.1.25和1 C.1和1 D.1和1.25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com