
 请证明爱尔可斯定理:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形.
请证明爱尔可斯定理:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 证明:连接AE、CE、CD,M是AE的中点,N是CE的中点,H是CD的中点,连接QM、QN、PM、CN、PH、GH,
证明:连接AE、CE、CD,M是AE的中点,N是CE的中点,H是CD的中点,连接QM、QN、PM、CN、PH、GH,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
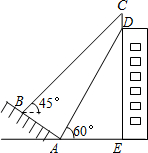 如图,某校一幢教学大楼的顶部竖有一块宣传牌CD=2米.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
如图,某校一幢教学大楼的顶部竖有一块宣传牌CD=2米.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 反比例函数y=
反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 由物理学知识可知:在力F(牛)的作用下,物体会在力F的方向发生位移S(米),力F所做的功W(焦),满足W=FS,当W为定值时,F与S之间的函数图象如图.
由物理学知识可知:在力F(牛)的作用下,物体会在力F的方向发生位移S(米),力F所做的功W(焦),满足W=FS,当W为定值时,F与S之间的函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com