
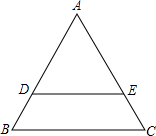
 如图,已知△ABC是等边三角形,D、E分别是AB、AC边上的点,且DB=EC.
如图,已知△ABC是等边三角形,D、E分别是AB、AC边上的点,且DB=EC.分析 (1)作点E关于直线BC的对称点E′,连接DE′,DE′与直线BC的交点P的位置即为所求.
(2)连接CE′,由对称轴的性质得EC=EC′,进而求得DB=E′C,然后根据AAS证得△PBD≌△PCE′,根据全等三角形对应边相等从而证得结论.
解答 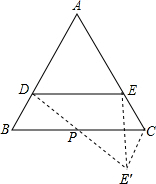 解;(1)如图,作点E关于直线BC的对称点E′,连接DE′,DE′与直线BC的交点P的位置即为所求.
解;(1)如图,作点E关于直线BC的对称点E′,连接DE′,DE′与直线BC的交点P的位置即为所求.
(2)连接CE′,由对称轴的性质得EC=EC′,
∵DB=EC,
∴DB=E′C,
∵△ABC是等边三角形,
∴∠B=∠ECB=∠E′CP=60°,
在△PBD和△PCE′中,
$\left\{\begin{array}{l}{∠B=∠E′CP}\\{∠BPD=∠CPE′}\\{DB=E′C}\end{array}\right.$
∴△PBD≌△PCE′(AAS),
∴PB=PC.
点评 本题考查的是轴对称-最短路线问题,三角形全等的判定和性质,涉及正三角形的性质、两点之间线段最短等知识.


科目:初中数学 来源: 题型:解答题
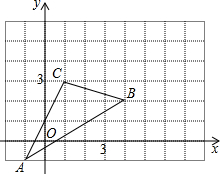 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$的图象上 | B. | y=-$\frac{1}{x}$的图象上 | C. | y=$\frac{2}{x}$的图象上 | D. | y=-$\frac{2}{x}$的图象上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
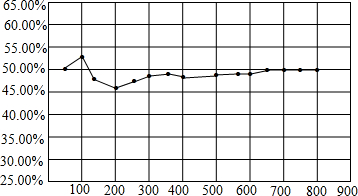 在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化析线图如图所示,则符合这一结果的实验最有可能的是( )
在对某次实验数据整理过程中,某个事件出现的频率随实验次数变化析线图如图所示,则符合这一结果的实验最有可能的是( )| A. | 抛一个质地均匀的正六面体骰子,向上的面点数是4 | |
| B. | 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 | |
| C. | 一副的普通扑克牌洗匀后,从中任取一张牌的花色是红桃 | |
| D. | 抛硬币实验中关注正面出现的概率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
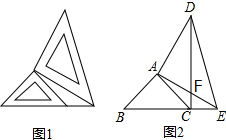 两块不相等的等腰直角三角形如图1放置,图2是它们抽象出的几何图形,点B、C、E在同一条直线上,连接CD,AE、CD交于点F,请你在不添加线段或字母的情况下:
两块不相等的等腰直角三角形如图1放置,图2是它们抽象出的几何图形,点B、C、E在同一条直线上,连接CD,AE、CD交于点F,请你在不添加线段或字母的情况下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com