
【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 为⊙
为⊙ ![]() 的弦,过点
的弦,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() ,交
,交 ![]() 的延长线于点
的延长线于点 ![]() .点
.点 ![]() 在
在 ![]() 上,且
上,且 ![]() .
.
(1)求证:直线 ![]() 是⊙
是⊙ ![]() 的切线;
的切线;
(2)若 ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)证明:连结OB.
∵OA=OB,∴∠A=∠OBA,
又∵BC=PC,
∴∠P=∠CBP,
∵OP⊥AD,
∴∠A+∠P=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=180°﹣(∠OBA+∠CBP)=90°,
∵点B在⊙O上,
∴直线BC是⊙O的切线,
(2)解:如图,
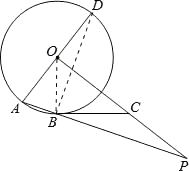
连结DB.
∵AD是⊙O的直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△AOP,
∴ ![]() ,即
,即 ![]() ,AP=9,
,AP=9,
∴BP=AP﹣BA=9﹣2=7.
【解析】(1)由OA=OB,得到∠A=∠OBA,又BC=PC,得到∠P=∠CBP,由OP⊥AD和三角形内角和定理,求出∠OBC=90°,得到直线BC是⊙O的切线;(2)由AD是⊙O的直径,得到两个直角三角形Rt△ABD∽Rt△AOP,得到比例,求出AP的值,得到BP=AP﹣BA的值.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BE平分∠ABC交AD于点E,已知BC=7cm,CD=5cm,∠D=60°,则下列说法错误的是( )

A. ∠C=120°B. ∠BED=120°C. AE=5cmD. ED=2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护环境,某市污水处理厂决定先购买A,B两型污水处理设备共20台,对周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知2台A型污水处理设备和1台B型污水处理设备每周可以处理污水680吨,4台A型污水处理设备和3台B型污水处理设备每周可以处理污水1560吨.
(1)求A、B两型污水处理设备每周每台分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案.
(3)如果你是厂长,从节约资金的角度来谈谈你会选择哪种方案并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图像与
的图像与 ![]() 轴交于点
轴交于点 ![]() 、
、 ![]() ,与
,与 ![]() 轴交于点
轴交于点 ![]() .
.
(1)求二次函数的表达式;
(2)设上述抛物线的对称轴 ![]() 与
与 ![]() 轴交于点
轴交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() 于
于 ![]() ,
, ![]() 为线段
为线段 ![]()
上一点, ![]() 为
为 ![]() 轴负半轴上一点,以
轴负半轴上一点,以 ![]() 、
、 ![]() 、
、 ![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似;
相似;
满足条件的 ![]() 点有且只有一个时,求
点有且只有一个时,求 ![]() 的取值范围;
的取值范围;
②若满足条件的 ![]() 点有且只有两个,直接写出
点有且只有两个,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() ,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:![]() ;
;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com