
【题目】定义:形如y=|G|(G为用自变量表示的代数式)的函数叫做绝对值函数.
例如,函数y=|x﹣1|,y=![]() ,y=|﹣x2+2x+3|都是绝对值函数.
,y=|﹣x2+2x+3|都是绝对值函数.
绝对值函数本质是分段函数,例如,可以将y=|x|写成分段函数的形式:![]() .
.
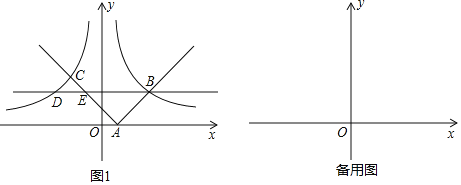
探索并解决下列问题:
(1)将函数y=|x﹣1|写成分段函数的形式;
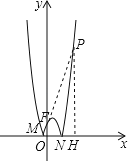
(2)如图1,函数y=|x﹣1|的图象与x轴交于点A(1,0),与函数y=![]() 的图象交于B,C两点,过点B作x轴的平行线分别交函数y=
的图象交于B,C两点,过点B作x轴的平行线分别交函数y=![]() ,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
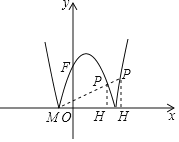
(3)已知函数y=|﹣x2+2x+3|的图象与y轴交于F点,与x轴交于M,N两点(点M在点N的左边),点P在函数y=|﹣x2+2x+3|的图象上(点P与点F不重合),PH⊥x轴,垂足为H.若△PMH与△MOF相似,请直接写出所有符合条件的点P的坐标.
【答案】(1)![]() ;(2)见解析;(3)P的坐标为(6,21),(
;(2)见解析;(3)P的坐标为(6,21),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)根据题中规定的写法写出即可.
(2)根据题意分别得出B、C、E、D的坐标,根据对应边成比例且夹角相等即可证明相似.
(3)根据题意先算出F、M、N的坐标,再利用设坐标点的方法,分类讨论,根据相似对应边成比例代入求解即可.
(1)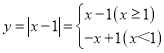 ;
;
(2)∵函数y=|x﹣1|与函数![]() 的图象交于B,C,过点B作x轴的平行线分别交函数
的图象交于B,C,过点B作x轴的平行线分别交函数![]() ,y=|x﹣1|的图象于D,E两点.
,y=|x﹣1|的图象于D,E两点.
∴根据条件得各点坐标为:B(3,2),C(﹣2,3),E(﹣1,2),D(﹣3,2).
∴BE=3﹣(﹣1)=4,DE=﹣1﹣(﹣3)=2,AE=![]() ,CE=
,CE=![]() ,
,
∴在△AEB和△CED中,∠AEB=∠CED,![]() ,
,
∴△PMB∽△PNA.
(3)P的坐标为(6,21),(![]() ,
, ![]() ),(
),(![]() ,
,![]() ).
).
当x=0时,y=|﹣x2+2x+3|=3,∴F(0,3).
当y=0时,|﹣x2+2x+3|=0,∴x1=﹣1,x2=3,∴M(﹣1,0),N(3,0).
由题意得y=|﹣x2+2x+3|=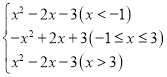 ,
,
设P的横坐标为x,
当x<﹣1时,由题意得P(x,x2﹣2x﹣3),
若△PMH∽△FMO, ![]() ,
,![]() .
.
解得x1=﹣1(舍去),x2=0(舍去).
若△PMH∽△MFO, ![]() ,
,![]() .
.
解得x1=﹣1(舍去),x2=![]() (舍去).
(舍去).
当﹣1<x<3时,由题意得P(x,﹣x2+2x+3),
若△PMH∽△MFO,![]() ,
,![]() .
.
解得x1=﹣1(舍去),x2=![]() .
.
∴P的坐标为(![]() ,
,![]() ).
).
若△PMH∽△MFO,![]() ,
,![]() .
.
解得x1=﹣1(舍去),x2=0(舍去).
当x>3时,由题意P(x,x2﹣2x﹣3),
若△PMH∽△FMO,![]() ,
,![]() .
.
解得x1=﹣1(舍去),x2=6.
∴P的坐标为(6,21).
若△PMH∽△MFO,![]() ,
,![]() .
.
解得 x1=﹣1(舍去),x2=![]() .
.
∴P的坐标为(![]() ,
,![]() ).
).
综上:P的坐标为(6,21),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】某路段上有A,B两处相距近200m且未设红绿灯的斑马线.为使交通高峰期该路段车辆与行人的通行更有序,交通部门打算在汽车平均停留时间较长的一处斑马线上放置移动红绿灯.图1,图2分别是交通高峰期来往车辆在A,B斑马线前停留时间的抽样统计图.根据统计图解决下列问题:
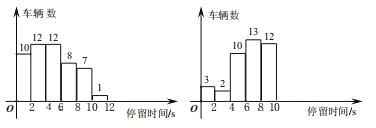
(1)若某日交通高峰期共有350辆车经过A斑马线,请估计该日停留时间为10s~12s的车辆数,以及这些停留时间为10s~12s的车辆的平均停留时间;(直接写出答案)
(2)移动红绿灯放置在哪一处斑马线上较为合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,全省各地市的2019年初中毕业升学体育考试工作正依照某省教育厅的具体要求在有条不紊的进行当中,某中学在正式考试前,为了让同学们在中招体育考试中获得理想成绩,同时为了了解学生的当前水平,按批次进行了模拟考试,并随机抽取若干名学生问卷调查,现将调查结果绘制成如下不完整的统计图表:
组别 | 成绩范围x(分) | 频数(人数) |
A | 60<x≤70 | 54 |
B | 50<x≤60 | m |
C | 40<x≤50 | n |
D | 30<x≤40 | 6 |
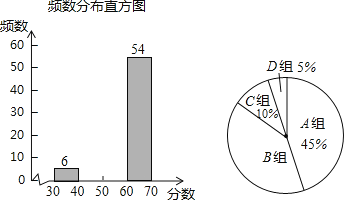
(1)这次调查的总人数有 人,表中的m= ,n= ;
(2)扇形统计图中B组对应的圆心角为 °;
(3)请补全频数分布直方图;
(4)若该校九年级共有学生2700名,且都参加了正式的初中毕业升学体育考试,小华也参加了这次考试并得了67分,若规定60分以上为优秀,体育老师想要在获得优秀的学生中随机抽出1名,作为学生代表向学弟学妹们传授经验,求抽到小华的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
(1)求证:CD是⊙O的切线;
(2)E为![]() 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=
的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=![]() ,BE=BG,EG=3
,BE=BG,EG=3![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
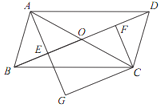
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①相等的弦所对的圆心角相等;②对角线相等的四边形是矩形;③正六边形的中心角为60°;④对角线互相平分且相等的四边形是菱形;⑤计算![]() 的结果为7;⑥函数y=
的结果为7;⑥函数y=![]() 的自变量x的取值范围是x>﹣1;⑦
的自变量x的取值范围是x>﹣1;⑦![]() 的运算结果是无理数.其中正确的是____(填序号即可)
的运算结果是无理数.其中正确的是____(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(6,0),点B的坐标为(0,2),点M从点A出发沿x轴负方向以每秒3cm的速度移动,同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.
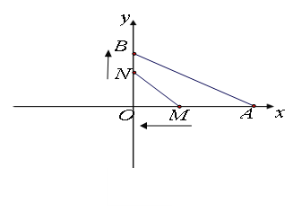
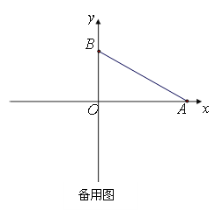
(1)若点M在线段OA上,试问当t为何值时,△ABO与以点O、M、N为顶点的三角形相似?
(2)若直线y=x与△OMN外接圆的另一个交点是点C.
①试说明:当0<t<2时,OM、ON、OC在移动过程满足OM+ON=![]() OC;
OC;
②试探究:当t>2时,OM、ON、OC之间的数量关系是否发生变化,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com