
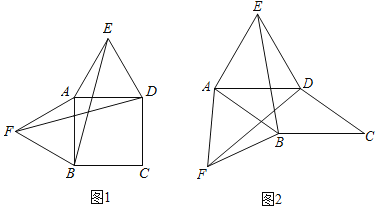
【题目】如图,以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接BE、DF.
(1)当四边形ABCD为正方形时(如图1),则线段BE与DF的数量关系是 .
(2)当四边形ABCD为平行四边形时(如图2),问(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)BE=DF(或相等);(2)成立.证明见解析.
【解析】
(1)根据正方形的性质和等边三角形性质得:AB=AD,∠BAD=90°,AF=AB,AE=AD,∠BAF=∠DAE=60°,再根据全等三角形判定和性质即可.
(2)先利用平行四边形性质和等边三角形性质,再运用全等三角形判定和性质即可.
解:(1)BE=DF(或相等)如图1,
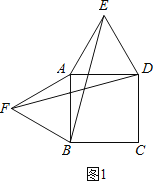
∵四边形ABCD为正方形
∴AB=AD,∠BAD=90°
∵△ABF、△ADE都是等边三角形
∴AF=AB,AE=AD,∠BAF=∠DAE=60°
∴∠BAE=∠BAD+∠DAE=150°,∠DAF=∠BAD+∠BAF=150°
∴∠BAE=∠DAF
∵AB=AF=AE=AD
∴△ABE≌△AFD(SAS)
∴BE=DF
故答案为:BE=DF或相等;
(2)成立.
证明:如图2,
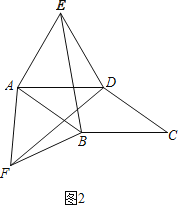
∵△AFB为等边三角形
∴AF=AB,∠FAB=60°
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE.
在△AFD和△ABE中,
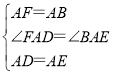 ,
,
∴△AFD≌△ABE(SAS),
∴BE=DF.


科目:初中数学 来源: 题型:
【题目】在![]() 中,点
中,点![]() 在边
在边![]() 上,联结
上,联结![]() .
.
![]() 如图,将
如图,将![]() 沿着
沿着![]() 翻折,点
翻折,点![]() 的对应点是点
的对应点是点![]() ,若
,若![]() 平分
平分![]() ,则
,则![]() 的值等于 ;
的值等于 ;

![]() 若
若![]() .将
.将![]() 绕着点
绕着点![]() 旋转,使得点
旋转,使得点![]() 的对应点
的对应点![]() 落在边
落在边![]() 上,点
上,点![]() 的对应点分别是点
的对应点分别是点![]() ,则
,则![]() 的面积等于 .
的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.

(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
查看答案和解析>>
科目:初中数学 来源: 题型:
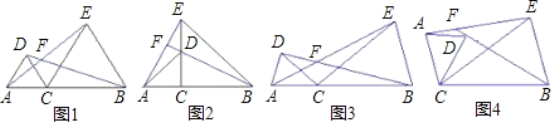
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB=______,如图2,若∠ACD=90°,则∠AFB=______,如图3,若∠ACD=α,则∠AFB=______(用含α的式子表示);
(2)设∠ACD=α,将图3中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图4,试探究∠AFB与α的数量关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
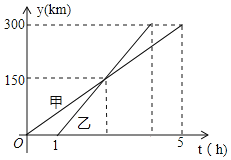
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.
(1)求乙车离开A城的距离y关于t的函数解析式;
(2)求乙车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为( )

A. 36° B. 45° C. 60° D. 72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的横坐标为3.
的横坐标为3.

(1)直接写出![]() 值________;
值________;
(2)当![]() 取何值时,
取何值时,![]() ?
?
(3)在![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com