
【题目】已知点C是线段AB的中点
(1)如图,若点D在线段CB上,且BD=1.5厘米,AD=6.5厘米,求线段CD的长度;
![]()
(2)若将(1)中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
【答案】(1)CD=2.5厘米;(2)CD=4厘米.
【解析】
根据BD+AD=AB可求出AB的长,利用中点的定义可求出BC的长,根据CD=BC-BD求出CD的长即可;(2)根据题意画出图形,利用线段中点的定义及线段的和差关系求出CD的长即可.
(1)∵BD=1.5厘米,AD=6.5厘米,
∴AB=BD+AD=8(厘米),
∵点C是线段AB的中点,
∴BC=![]() AB=4(厘米)
AB=4(厘米)
∴CD=BC-BD=2.5(厘米).
(2)当点D在线段CB的延长线上时,如图所示:
∵BD=1.5厘米,AD=6.5厘米,
∴AB=AD-BD=5(厘米),
∵点C是线段AB的中点,
∴BC=![]() AB=2.5(厘米)
AB=2.5(厘米)
∴CD=BC+BD=4(厘米)
![]()


科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠C=90°,点O在AC上,以AO为半径的⊙O交AB于D, BD的垂直平分线交BD于F,交BC于E,连接DE.

(1)求证:DE是⊙O的切线;
(2)若∠B=30°,BC=![]() ,且AD∶DF=1∶2,求⊙O的直径.
,且AD∶DF=1∶2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
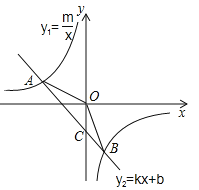
【题目】如图,已知反比例函数y1=![]() 的图像与一次函数y2=kx+b的图象交于两点A(-2,1)、B(a,-2).
的图像与一次函数y2=kx+b的图象交于两点A(-2,1)、B(a,-2).
(1)求反比例函数和一次函数的解析式;
(2)若一次函数y2=kx+b的图象交y轴于点C,求△AOB的面积(O为坐标原点);
(3)求使y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当下药品价格过高已成为一大社会问题,为整顿药品市场、降低药品价格,有关部门规定:市场流通药品的零售价格不得超过进价的15%.根据相关信息解决下列问题:
(1)甲乙两种药品每盒的出厂价格之和为6.6元.经过若干中间环节,甲种药品每盒的零售价格比出厂价格的5倍少2.2元,乙种药品每盒的零售价格是出厂价格的6倍,两种药品每盒的零售价格之和为33.8元.那么甲、乙两种药品每盒的零售价格分别是多少元?
(2)实施价格管制后,某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的
价格销售给医院,医院根据实际情况决定:对甲种药品每盒加价15% ,对乙种药品每盒加
价10%后零售给患者.实际进药时,这两种药品均以每10盒为1箱进行包装.近期该医院
准备从经销商处购进甲乙两种药品共100箱,其中乙种药品不少于40箱,要求销售这批药
品的总利润不低于900元.请问如何搭配才能使医院获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点O为原点,A点表示数a,B点表示数b,且a、b满足|a+2|+|b-4|=0;
![]()
(1)点A表示的数为 ;点B表示的数为 ;
(2)如果M、N为数轴上两个动点.点M从点A出发,速度为每秒1个单位长度;点N从点B出发,速度为点A的3倍,它们同时向左运动.
①当运动2秒时,点M、N对应的数分别是 、 .
②当运动t秒时,点M、N对应的数分别是 、 .(用含t的式子表示)
③运动多少秒时,点M、N、O中恰有一个点为另外两个点所连线段的中点?(可以直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某菜农在蔬菜基地搭建了一个横截面为圆弧形的蔬菜大棚,大棚的跨度弦AB的长为![]() 米,大棚顶点C离地面的高度为2.3米.
米,大棚顶点C离地面的高度为2.3米.
(1)求该圆弧形所在圆的半径;
(2)若该菜农的身高为1.70米,则他在不弯腰的情况下,横向活动的范围有几米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式分解的方法,其中运用公式法即运用平方差公式:a2-b2=(a+b)(a-b)和完全平方公式:a2±2ab+b2=(a±b)2进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+8x+7
=x2+8x+16-16+7
=(x+4)2-9
=(x+4+3)(x+4-3)
=(x+7)(x+1)
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将x2+2x-3化成a(x+m)2+n的形式为_______;
(2)请你利用上述方法因式分解:
①x2+6x+8;
②x2-6x-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD,则D点坐标是_______;在y轴上有一个动点M,当
与x轴、y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD,则D点坐标是_______;在y轴上有一个动点M,当![]() 的周长值最小时,则这个最小值是_______.
的周长值最小时,则这个最小值是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com