先阅读命题及证明思路,再解答下列问题.
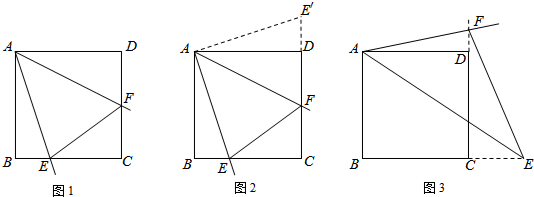
命题:如图1,在正方形ABCD中,已知:∠EAF=45°,角的两边AE、AF分别与BC、CD相交于点E、F,连接EF.求证:EF=BE+DF.
证明思路:
如图2,将△ABE绕点A逆时针旋转90°至△ADE′.∵AB=AD,∠BAD=90°,∴AB与AD重合.∵∠ADC=∠B=90°,∴∠FDE′=180°,点F、D、E′是一条直线.
根据SAS,得证△AEF≌△AFE′,得EF=E′F=E′D+DF=BE+DF.
(1)特例应用
如图1,命题中,如果BE=2,DF=3,求正方形ABCD的边长.
(2)类比变式
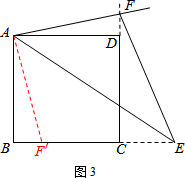
如图3,在正方形ABCD中,已知∠EAF=45°,角的两边AE、AF分别与BC、CD的延长线相交于点E、F,连接EF.写出EF、BE、DF之间的关系式,并证明你的结论.
(3)拓展深入
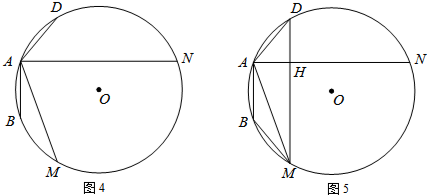
如图4,在⊙O中,AB、AD是⊙O的弦,且AB=AD,M、N是⊙O上的两点,∠MAN=
∠BAD.
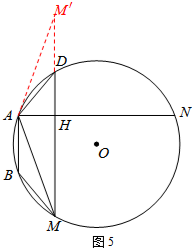
①如图5,连接MN、MD,求证:MH=BM+DH,DM⊥AN;
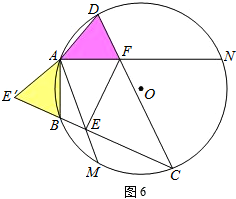
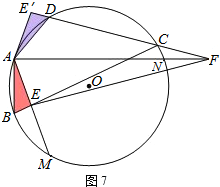
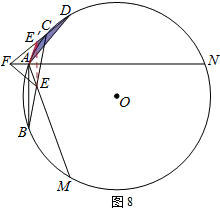
②若点C在
(点C不与点A、D、N、M重合)上,连接CB、CD分别交AM、AN或其延长线于点E、F,直接写出EF、BE、DF之间的等式关系.






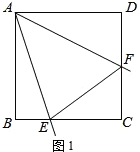




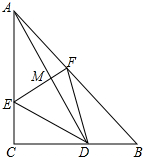 如图,D是等腰直角△ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,BC=2.
如图,D是等腰直角△ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,BC=2.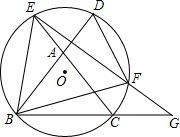 如图,△ABC是等边三角形,⊙O过点B、C,且与BA、CA的延长线分别交于点D、E,弦DF∥AC,EF的延长线交BC的延长线于点G.求证:△BEF是等边三角形.
如图,△ABC是等边三角形,⊙O过点B、C,且与BA、CA的延长线分别交于点D、E,弦DF∥AC,EF的延长线交BC的延长线于点G.求证:△BEF是等边三角形.