
【题目】如图,正方形ABCD中,点E、F分别在AB、CD上,DG⊥EF于点H,交BC于点G,点P在线段BG上.若∠PEF=45°,AE=CG=5,PG=5,则EP=____.

【答案】5![]() .
.
【解析】
过点F作FM⊥AB于点M,连接PF、PM,则FM=AD,AM=DF,由ASA证明△MCE≌△CDG,得出ME=CG=5,得出AM=DF=10,证明E、M、P、F四点共圆,得出∠EPF=∠FME=90°,证出△PEF是等腰直角三角形,得出EP=FP,证明△BPE≌△CFP,得出BE=CP=10,求出AB=AE+BE=15,BP=5,在Rt△BPE中,由勾股定理即可得出结果.
过点F作FM⊥AB于点M,连接PF、PM,如图所示:
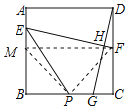
则FM=AD,AM=DF,∠FME=∠MFD=90°,
∵DG⊥EF,
∴∠MFE=∠CDG,
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=DC=AD,
∴FM=DC,
在△MCE和△CDG中, ,
,
∴△MCE≌△CDG(ASA),
∴ME=CG=5,
∴AM=DF=10,
∵CG=PG=5,
∴CP=10,
∴AM=CP,
∴BM=BP,
∴△BPM是等腰直角三角形,
∴∠BMP=45°,
∴∠PMF=45°,
∵∠PEF=45°=∠PMF,
∴E、M、P、F四点共圆,
∴∠EPF=∠FME=90°,
∴△PEF是等腰直角三角形,
∴EP=FP,
∵∠BEP+∠BPE=90°,∠BPE+∠CPF=90°,
∴∠BEP=∠CPF,
在△BPE和△CFP中,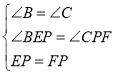 ,
,
∴△BPE≌△CFP(AAS),
∴BE=CP=10,
∴AB=AE+BE=15,
∴BP=5,
在Rt△BPE中,由勾股定理得:EP=![]() =5
=5![]() ;
;
故答案为:5![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(﹣3,0),(0,﹣3).
(1)求抛物线的表达式.
(2)已知点(m,k)和点(n,k)在此抛物线上,其中m≠n,请判断关于t的方程t2+mt+n=0是否有实数根,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
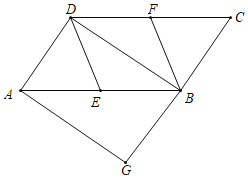
【题目】如图,在平行四边形ABCD中,点E、F分别为边AB、CD的中点,BD是平行四边形ABCD的对角线,AG∥BD交CB的延长线于点G
(1)求证:四边形BEDF是平行四边形;
(2)若AE=DE,则四边形AGBD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
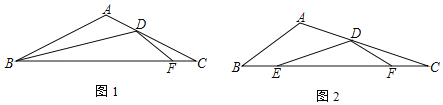
【题目】在△ABC中,点E、F在边BC上,点D在边AC上,连接ED、DF,![]() =m,∠A=∠EDF=120°
=m,∠A=∠EDF=120°
(1)如图1,点E、B重合,m=1时
①若BD平分∠ABC,求证:CD2=CFCB;
②若![]() ,则
,则![]() = ;
= ;
(2)如图2,点E、B不重合.若BE=CF,![]() =m,
=m,![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=ax+b与双曲线![]() 交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
(1)①求k的值和点C的坐标;②求直线l的表达式;
(2)过点B作y轴的垂线与直线AC交于点D,经过点C的直线与直线BD交于点E.若30°≤∠CED≤45°,直接写出点E的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
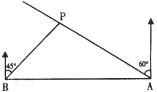
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
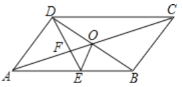
【题目】如图,ABCD的对角线AC、BD交于点O,DE平分∠ADC交AB于点E,∠BCD=60°,AD=![]() AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的结论是_____.
AB,连接OE.下列结论:①SABCD=ADBD;②DB平分∠CDE;③AO=DE;④S△ADE=5S△OFE,其中正确的结论是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com