
ЁОЬтФПЁПЃЈжЊЪЖЩњГЩЃЉЮвУЧвбОжЊЕРЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФУцЛ§ПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЎР§ШчЭМ1ПЩвдЕУЕНЃЈa+bЃЉ2ЃНa2+2ab+b2ЃЌЛљгкДЫЃЌЧыНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉИљОнЭМ2ЃЌаДГівЛИіДњЪ§КуЕШЪНЃКЁЁ ЁЁЃЎ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕУЕНЕФНсТлЃЌНтОіЯТУцЕФЮЪЬтЃКШєa+b+cЃН10ЃЌab+ac+bcЃН35ЃЌдђa2+b2+c2ЃНЁЁ ЁЁЃЎ
ЃЈ3ЃЉаЁУїЭЌбЇгУЭМ3жаxеХБпГЄЮЊaЕФе§ЗНаЮЃЌyеХБпГЄЮЊbЕФе§ЗНаЮЃЌzеХПэЁЂГЄЗжБ№ЮЊaЁЂbЕФГЄЗНаЮжНЦЌЦДГівЛИіУцЛ§ЮЊЃЈ2a+bЃЉЃЈa+2bЃЉГЄЗНаЮЃЌдђx+y+zЃНЁЁ ЁЁЃЎ
ЃЈжЊЪЖЧЈвЦЃЉЃЈ4ЃЉЪТЪЕЩЯЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФЬхЛ§вВПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЌЭМ4БэЪОЕФЪЧвЛИіБпГЄЮЊxЕФе§ЗНЬхЭкШЅвЛИіаЁГЄЗНЬхКѓжиаТЦДГЩвЛИіаТГЄЗНЬхЃЌЧыФуИљОнЭМ4жаЭМаЮЕФБфЛЏЙиЯЕЃЌаДГівЛИіДњЪ§КуЕШЪНЃКЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЛЃЈ2ЃЉ30ЃЛЃЈ3ЃЉ9ЃЛЃЈ4ЃЉx3ЉxЃНЃЈx+1ЃЉЃЈxЉ1ЃЉx
ЁОНтЮіЁП
ЃЈ1ЃЉвРОне§ЗНаЮЕФУцЛ§ЃНЃЈa+b+cЃЉ2ЃЛе§ЗНаЮЕФУцЛ§ЃНa2+b2+c2+2ab+2ac+2bcЃЌПЩЕУЕШЪНЃЛ
ЃЈ2ЃЉвРОнa2+b2+c2ЃНЃЈa+b+cЃЉ2Љ2abЉ2acЉ2bcЃЌНјааМЦЫуМДПЩЃЛ
ЃЈ3ЃЉвРОнЫљЦДЭМаЮЕФУцЛ§ЮЊЃКxa2+yb2+zabЃЌЖјЃЈ2a+bЃЉЃЈa+2bЃЉЃН2a2+4ab+ab+2b2ЃН2a2+5b2+2abЃЌМДПЩЕУЕНxЃЌyЃЌzЕФжЕЃЎ
ЃЈ4ЃЉИљОндМИКЮЬхЕФЬхЛ§ЃНаТМИКЮЬхЕФЬхЛ§ЃЌСаЪНПЩЕУНсТлЃЎ
ЃЈ1ЃЉгЩЭМ2ЕУЃКе§ЗНаЮЕФУцЛ§ЃНЃЈa+b+cЃЉ2ЃЛе§ЗНаЮЕФУцЛ§ЃНa2+b2+c2+2ab+2ac+2bcЃЌ
ЁрЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЌ
ЙЪД№АИЮЊЃКЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЛ
ЃЈ2ЃЉЁпЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЌ
Ёпa+b+cЃН10ЃЌab+ac+bcЃН35ЃЌ
Ёр102ЃНa2+b2+c2+2ЁС35ЃЌ
Ёрa2+b2+c2ЃН100Љ70ЃН30ЃЌ
ЙЪД№АИЮЊЃК30ЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃКЃЈ2a+bЃЉЃЈa+2bЃЉЃНxa2+yb2+zabЃЌ
Ёр2a2+5ab+2b2ЃНxa2+yb2+zabЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрx+y+zЃН9ЃЌ
ЙЪД№АИЮЊЃК9ЃЛ
ЃЈ4ЃЉЁпдМИКЮЬхЕФЬхЛ§ЃНx3Љ1ЁС1xЃНx3ЉxЃЌ
аТМИКЮЬхЕФЬхЛ§ЃНЃЈx+1ЃЉЃЈxЉ1ЃЉxЃЌ
Ёрx3ЉxЃНЃЈx+1ЃЉЃЈxЉ1ЃЉxЃЎ
ЙЪД№АИЮЊЃКx3ЉxЃНЃЈx+1ЃЉЃЈxЉ1ЃЉxЃЎ


 УЂЙћНЬИЈДяБъВтЪдОэЯЕСаД№АИ
УЂЙћНЬИЈДяБъВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцЭМаЮЩЯЕФШЮвтСНЕу![]() ЃЌ
ЃЌ![]() ЃЌШчЙћОЙ§ФГжжБфЛЛЃЈШчЃКЦНвЦЁЂа§зЊЁЂжсЖдГЦЕШЃЉЕУЕНаТЭМаЮЩЯЕФЖдгІЕу
ЃЌШчЙћОЙ§ФГжжБфЛЛЃЈШчЃКЦНвЦЁЂа§зЊЁЂжсЖдГЦЕШЃЉЕУЕНаТЭМаЮЩЯЕФЖдгІЕу![]() ЃЌ
ЃЌ![]() ЃЌБЃГж
ЃЌБЃГж![]() ЃЌЮвУЧАбетжжЖдгІЕуСЌЯпЯрЕШЕФБфЛЛГЦЮЊЁАЭЌВНБфЛЛЁБЃЎЖдгкШ§жжБфЛЛЃК
ЃЌЮвУЧАбетжжЖдгІЕуСЌЯпЯрЕШЕФБфЛЛГЦЮЊЁАЭЌВНБфЛЛЁБЃЎЖдгкШ§жжБфЛЛЃК
ЂйЦНвЦЁЂЂка§зЊЁЂЂлжсЖдГЦЃЌ
ЦфжавЛЖЈЪЧЁАЭЌВНБфЛЛЁБЕФга________ЃЈЬюађКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕдкМзЕигавЛЙЄГЇЃЈМђГЦМзГЇЃЉЩњВњФГВњЦЗЃЌ2017ФъЕФФъВњСПЙ§ЭђМўЃЌ2018ФъМзГЇОЙ§ММЪѕИФдьЃЌШеОљЩњВњЕФИУВњЦЗЪ§ЪЧИУГЇ2017ФъЕФ2БЖЛЙЖр2Мў.
ЃЈ1ЃЉШєМзГЇ2018ФъЩњВњ200МўИУВњЦЗЫљашЕФЪБМфгы2017ФъЩњВњ99МўИУВњЦЗЫљашЕФЪБМфЯрЭЌЃЌдђ2017ФъМзГЇШеОљЩњВњИУВњЦЗЖрЩйМўЃП
ЃЈ2ЃЉгЩгкИУВњЦЗЩюЪмЙЫПЭЛЖгЃЌ2019ФъИУЦѓвЕдкввЕиНЈСЂаТГЇЃЈМђГЦввГЇЃЉЩњВњИУВњЦЗ.ввГЇЕФШеОљЩњВњЕФИУВњЦЗЪ§ЪЧМзГЇ2017ФъЕФ3БЖЛЙЖр4Мў.ЭЌФъИУЦѓвЕвЊЧѓМзЁЂввСНГЇЗжБ№ЩњВњmЃЌnМўВњЦЗЃЈМзГЇЕФШеОљВњСПгы2018ФъЯрЭЌЃЉЃЌm:nЃН14:25ЃЌШєМзЁЂввСНГЇЭЌЪБПЊЪМЩњВњЃЌЫЯШЭъГЩШЮЮёЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊОиаЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋЫќШЦзХЕу
ЃЌНЋЫќШЦзХЕу![]() АДЫГЪБеыЗНЯђа§зЊ
АДЫГЪБеыЗНЯђа§зЊ![]() ЖШ
ЖШ![]() ЕУЕНОиаЮ
ЕУЕНОиаЮ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЃЌ
ЃЌ![]() етСНБпЫљдкЕФжБЯпЗжБ№гы
етСНБпЫљдкЕФжБЯпЗжБ№гы![]() БпЫљдкЕФжБЯпЯрНЛгкЕу
БпЫљдкЕФжБЯпЯрНЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФГЄЮЊ________ЃЎ
ЕФГЄЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫЎЩЯжЮАВжИЛгЫў![]() ЮїВрСНЬѕКНЯп
ЮїВрСНЬѕКНЯп![]() ЁЂ
ЁЂ![]() ЩЯгаСНЫвбВТпЭЇ
ЩЯгаСНЫвбВТпЭЇ![]() гы
гы![]() ЫљдкКНЯпППНќ
ЫљдкКНЯпППНќ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЁЂ
ЁЂ![]() МфЕФОрРы
МфЕФОрРы![]() ЃЌЕу
ЃЌЕу![]() дкЕу
дкЕу![]() ЕФФЯЦЋЮї
ЕФФЯЦЋЮї![]() ЗНЯђЩЯЃЌЧв
ЗНЯђЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() дк
дк![]() ЕФББЦЋЖЋ
ЕФББЦЋЖЋ![]() ЗНЯђЩЯЃЎЧѓЃК
ЗНЯђЩЯЃЎЧѓЃК

![]() бВТпЭЇ
бВТпЭЇ![]() гыЫў
гыЫў![]() жЎМфЕФОрРы
жЎМфЕФОрРы![]() ЃЎЃЈНсЙћБЃСєИљКХЃЉ
ЃЎЃЈНсЙћБЃСєИљКХЃЉ
![]() вбжЊбВТпЭЇ
вбжЊбВТпЭЇ![]() ЕФЫйЖШУПаЁЪББШбВТпЭЇ
ЕФЫйЖШУПаЁЪББШбВТпЭЇ![]() Пь
Пь![]() ЃЌЕБСНЫвбВТпЭЇЭЌЪБЕНДяжИЛгЫў
ЃЌЕБСНЫвбВТпЭЇЭЌЪБЕНДяжИЛгЫў![]() ЕФе§ФЯЗНЯђЪБЃЌЧѓбВТпЭЇ
ЕФе§ФЯЗНЯђЪБЃЌЧѓбВТпЭЇ![]() ЕФЫйЖШЃЎ
ЕФЫйЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуCЮЊЯпЖЮABЩЯвЛЕуЃЌЗжБ№вдACЁЂBCЮЊБпдкЯпЖЮABЭЌВрзїЁїACDКЭЁїBCE,ЧвCA=CDЃЌCB=CEЃЌЁЯACD=ЁЯBCE=ІСЃЌжБЯпAEгыBDНЛгкЕуF.
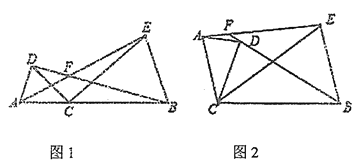
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌ
ЂйЧѓжЄAE= BD
ЂкЧѓЁЯAFB (гУКЌІСЕФДњЪ§ЪНБэЪО)
ЃЈ2ЃЉНЋЭМ1жаЕФЁїACDШЦЕуCЫГЪБеыа§зЊФГИіНЧЖШ(НЛЕуFжСЩйдкBDЁЂAEжаЕФвЛЬѕЯпЖЮЩЯ)ЃЌЕУЕНШчЭМ2ЫљЪОЕФЭМаЮЃЌШєЁЯAFB= 150ЁуЃЌЧыжБНгаДГіДЫЪБЖдгІЕФІСЕФДѓаЁ(ВЛгУжЄУї)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯвЛЕуЃЌЕу
БпЩЯвЛЕуЃЌЕу![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯСНЕуЃЌЧв
БпЩЯСНЕуЃЌЧв![]() ЃЌзїЕу
ЃЌзїЕу![]() Йигк
Йигк![]() ЕФЖдГЦЕуЕу
ЕФЖдГЦЕуЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.

ЃЈ1ЃЉвРЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉВТЯы![]() ______ЁуЃЌВЂжЄУїЃЛ
______ЁуЃЌВЂжЄУїЃЛ
ЃЈ3ЃЉВТЯыЯпЖЮ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФЪ§СПЙиЯЕ______ЃЌВЂжЄУї.
ЕФЪ§СПЙиЯЕ______ЃЌВЂжЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНЉx+7ЕФЭМЯѓгые§БШР§КЏЪ§yЃН![]() xЕФЭМЯѓНЛгкЕуAЃЌЕуPЃЈtЃЌ0ЃЉЪЧxе§АыжсЩЯЕФвЛИіЖЏЕуЃЎ
xЕФЭМЯѓНЛгкЕуAЃЌЕуPЃЈtЃЌ0ЃЉЪЧxе§АыжсЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊЃЈЁЁ ЁЁЃЌЁЁ ЁЁЃЉЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгPAЃЌШєЁїAOPЪЧЕШбќШ§НЧаЮЃЌЧѓЕуPЕФзјБъЃК
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌЗжБ№НЛyЃН![]() xКЭyЃНЉx+7ЕФЭМЯѓгкЕуBЃЌCЃЎЪЧЗёДцдке§ЪЕЪ§ЃЌЪЙЕУBCЃН
xКЭyЃНЉx+7ЕФЭМЯѓгкЕуBЃЌCЃЎЪЧЗёДцдке§ЪЕЪ§ЃЌЪЙЕУBCЃН![]() OAЃЌШєДцдкЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
OAЃЌШєДцдкЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЬНОПЃК
ШчЭМ1ЃЌХзЮяЯпy=Љ![]() x2+
x2+![]() x+
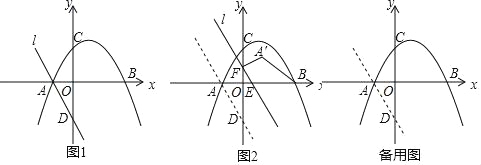
x+![]() гыxжсЗжБ№НЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкCЕуЃЎОЙ§ЕуAЕФжБЯпlгыyжсНЛгкЕуDЃЈ0ЃЌЉ
гыxжсЗжБ№НЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкCЕуЃЎОЙ§ЕуAЕФжБЯпlгыyжсНЛгкЕуDЃЈ0ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъМАжБЯпlЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпlДгЭМжаЕФЮЛжУГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиxжсЕФе§ЗНЯђдЫЖЏЃЌдЫЖЏжажБЯпlгыxжсНЛгкЕуEЃЌгыyжсНЛгкЕуFЃЌЕуA ЙигкжБЯпlЕФЖдГЦЕуЮЊAЁфЃЌСЌНгFAЁфЁЂBAЁфЃЌЩшжБЯпlЕФдЫЖЏЪБМфЮЊtЃЈtЃО0ЃЉУыЃЎЬНОПЯТСаЮЪЬтЃК
ЂйЧыжБНгаДГіAЁфЕФзјБъЃЈгУКЌзжФИtЕФЪНзгБэЪОЃЉЃЛ
ЂкЕБЕуAЁфТфдкХзЮяЯпЩЯЪБЃЌЧѓжБЯпlЕФдЫЖЏЪБМфtЕФжЕЃЌХаЖЯДЫЪБЫФБпаЮAЁфBEFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЬНОПЃКдкжБЯпlЕФдЫЖЏЙ§ГЬжаЃЌзјБъЦНУцФкЪЧЗёДцдкЕуPЃЌЪЙЕУвдPЃЌAЁфЃЌBЃЌEЮЊЖЅЕуЕФЫФБпаЮЮЊОиаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛ ШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com