
【题目】如图,一次函数y=﹣x+7的图象与正比例函数y=![]() x的图象交于点A,点P(t,0)是x正半轴上的一个动点.
x的图象交于点A,点P(t,0)是x正半轴上的一个动点.
(1)点A的坐标为( , );
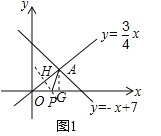
(2)如图1,连接PA,若△AOP是等腰三角形,求点P的坐标:
(3)如图2,过点P作x轴的垂线,分别交y=![]() x和y=﹣x+7的图象于点B,C.是否存在正实数,使得BC=
x和y=﹣x+7的图象于点B,C.是否存在正实数,使得BC=![]() OA,若存在求出t的值;若不存在,请说明理由.
OA,若存在求出t的值;若不存在,请说明理由.

【答案】(1)(4,3);(2)P(5,0)或(8,0)或(![]() ,0);(3)t=
,0);(3)t=![]() .
.
【解析】
(1)解方程组即可得到结论;
(2)根据勾股定理得到OA=![]() =5,当OP=OA=5时,△AOP是等腰三角形,当AP=OA=5时,△AOP是等腰三角形,当OP=PA时,△AOP是等腰三角形,于是得到结论;
=5,当OP=OA=5时,△AOP是等腰三角形,当AP=OA=5时,△AOP是等腰三角形,当OP=PA时,△AOP是等腰三角形,于是得到结论;
(3)由P(t,0),得到B(t,![]() t),C(t,﹣t+7),根据BC=
t),C(t,﹣t+7),根据BC=![]() OA,解方程即可得到结论.
OA,解方程即可得到结论.
解:(1)解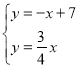 得
得![]() ,
,
∴点A的坐标为(4,3),
故答案为:(4,3);
(2)∵A(4,3),
∴OA=![]() =5,
=5,
当OP=OA=5时,△AOP是等腰三角形,
∴P(5,0),
当AP=OA=5时,△AOP是等腰三角形,
则OP=8,
∴P(8,0);
当OP=PA时,△AOP是等腰三角形,
则点P在OA的垂直平分线上,
如图1,设OA的垂直平分线交OA于H,
∴OH=![]() OA=
OA=![]() ,
,
过A作AG⊥x轴于G,
∴△OPH∽△OAG,
∴![]() ,
,
∴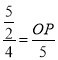 ,
,
∴OP=![]() ,
,
∴P(![]() ,0),
,0),
综上所述,P(5,0)或(8,0)或(![]() ,0);
,0);
(3)∵P(t,0),
∴B(t,![]() t),C(t,﹣t+7),
t),C(t,﹣t+7),
∵BC=![]() OA,
OA,
∴﹣t+7﹣![]() t=
t=![]() ×5或
×5或![]() t+t﹣7=
t+t﹣7=![]() ×5,
×5,
解得:t=﹣![]() 或t=
或t=![]() ,
,
∵t>0,
∴t=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°—∠ABC—2x°,则下列角中,大小为x°的角是

A.∠EFCB.∠ABCC.∠FDCD.∠DFC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:

(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,格点△ABC(顶点是网格线的交点)在平面直角坐标系中的位置如图所示.
(1)将△ABC先向下平移2个单位长度,再向右平移8个单位长度,画出平移后的△A1B1C1,并写出顶点B1的坐标;
(2)作△ABC关于y轴的对称图形△A2B2C2,并写出项点B2的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,AB=BC,E、M分别为AB、AC上的点,连接CE,BM交于点G,且BM⊥CE,O为AC的中点,连接BO交CE于点N.
(1)如图①,若AB=6,2MO=AM,求BM的长;
(2)如图②,连接OG、AG,若AG⊥OG,求证:AC=![]() BG.
BG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华的父亲计划修建一个矩形草坪,按![]() 的比例尺画出了草坪图(如图),他准备在草坪内栽种面积为
的比例尺画出了草坪图(如图),他准备在草坪内栽种面积为![]() 平方米的小矩形草皮,在草坪四周每隔
平方米的小矩形草皮,在草坪四周每隔![]() 厘米种一株小杜鹃,你能帮助小华的父亲算算他需购买多少块小矩形草皮与多少株杜鹃吗?
厘米种一株小杜鹃,你能帮助小华的父亲算算他需购买多少块小矩形草皮与多少株杜鹃吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列二元一次方程组解应用题
甲、乙两件服装的成本共500元,商店老板为获取利润,将甲服装按50%的利润定价,乙服装按40%利润定价,在实际出售时,应顾客要求,两件服装均按定价的9折出售,这样商店共获利157元,求若两件服装都打8折,商店共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魏晋时期的数学家刘徽首创割圆术.为计算圆周率建立了严密的理论和完善的算法.作圆内接正多边形,当正多边形的边数不断增加时,其周长就无限接近圆的周长,进而可用![]() 来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )
来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )

A. 0.5 B. 1 C. 3 D. π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com