
【题目】某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.
(1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m,n件产品(甲厂的日均产量与2018年相同),m:n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
【答案】(1)99件;(2)甲厂先完成任务,理由见详解.
【解析】
(1)设2017年甲厂日均生产该产品x件,根据2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同列得方程;
(2)先求出甲、乙两厂的日均生产数量,用含m的代数式表示n,再分别表示出甲、乙两厂的生产时间,进行比较即可得到答案.
(1)设2017年甲厂日均生产该产品x件,则2018年甲厂日均生产该产品(2x+2)件,
![]() ,
,
x=99,
经检验,x=99是原分式方程的解,
答:2017年甲厂日均生产该产品99件.
(2)2019年甲厂日均生产![]() 件,乙厂日均生产
件,乙厂日均生产![]() 件,
件,
∵m:n=14:25,
∴![]() ,
,
∴甲厂生产m个所需要的时间为: 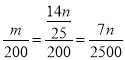 ,
,
乙厂生产n个所需要的时间为:![]()
∵![]() ,
,
∴甲厂先完成任务.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
截长补短法,是初中数学儿何题中一种输助线的添加方法,截长就是在长边上载取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.
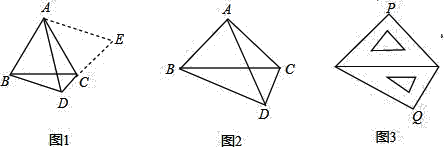
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD.连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.
根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是___________
(拓展延伸)
(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;
(知识应用)
(3)如图3,一副三角尺斜边长都为14cm,把斜边重叠摆放在一起,则两块三角尺的直角项点之间的距离PQ的长为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种单价为![]() 元的篮球,如果以单价
元的篮球,如果以单价![]() 元出售,那么每月可售出
元出售,那么每月可售出![]() 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高![]() 元,销售量相应减少
元,销售量相应减少![]() 个;
个;
某商场购进一种单价为![]() 元的篮球,如果以单价
元的篮球,如果以单价![]() 元出售,那么每月可售出
元出售,那么每月可售出![]() 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高![]() 元,销售量相应减少
元,销售量相应减少![]() 个;
个;
![]() 假设销售单价提高
假设销售单价提高![]() 元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含
元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含![]() 的代数式表示)
的代数式表示)
![]() 若商店准备获利
若商店准备获利![]() 元,则销售定价为多少元?商店应进货多少个?
元,则销售定价为多少元?商店应进货多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
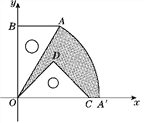
【题目】如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把这两块三角板放置在平面直角坐标系中,且OB=3![]() .
.
(1)若某反比例函数的图象的一个分支恰好经过点A,求这个反比例函数的解析式;
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好落在x轴上,点A落在点A′处,试求图中阴影部分的面积.(结果保留π)
【答案】(1)反比例函数的解析式为y=![]() ;(2)S阴影=6π-
;(2)S阴影=6π-![]() .
.
【解析】分析:(1)根据tan30°=![]() ,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=
,求出AB,进而求出OA,得出A的坐标,设过A的双曲线的解析式是y=![]() ,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
,把A的坐标代入求出即可;(2)求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OD、DC长,求出△ODC的面积,相减即可求出答案.
本题解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3![]() ,
,
∴AB=OB·tan 30°=3.
∴点A的坐标为(3,3![]() ).
).
设反比例函数的解析式为y=![]() (k≠0),
(k≠0),
∴3![]() =
=![]() ,∴k=9
,∴k=9![]() ,则这个反比例函数的解析式为y=
,则这个反比例函数的解析式为y=![]() .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=![]() ,即sin 30°=
,即sin 30°=![]() ,
,
∴OA=6.
由题意得:∠AOC=60°,S扇形AOA′=![]() =6π.
=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3![]() ,
,
∴OD=OC·cos 45°=3![]() ×
×![]() =
=![]() .
.
∴S△ODC=![]() OD2=
OD2=![]()
![]() =
=![]() .
.
∴S阴影=S扇形AOA′-S△ODC=6π-![]() .
.
点睛:本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积及等腰三角形的性质,本题属于中档题,难度不大,将不规则的图形的面积表示成多个规则图形的面积之和是解答本题的关键.
【题型】解答题
【结束】
26
【题目】矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
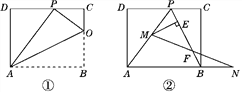
(1)如图①,已知折痕与边BC交于点O,连接AP,OP,OA.
① 求证:△OCP∽△PDA;
② 若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立一次函数关系解决问题:甲、乙两校为了绿化校园,甲校计划购买A种树苗,A种树苗每棵24元;乙校计划购买B种树苗,B种树苗每棵18元.两校共购买了35棵树苗.若购进B种树苗的数量少于A种树苗的数量,请给出一种两校总费用最少的方案,并求出该方案所需的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字﹣乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为一圆洞门.工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑,点A、B、C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AB=2![]() ,EF=
,EF=![]() ,
,![]() =120°.
=120°.
(1)求出圆洞门⊙O的半径;
(2)求立柱CE的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com