
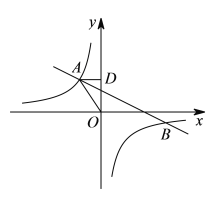
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
【答案】(1) 反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣
,一次函数的解析式为y=﹣![]() x+2.(2)x≤﹣2或0<x≤6.
x+2.(2)x≤﹣2或0<x≤6.
【解析】
(1)根据S△AOD=3可得AD=2,根据反比例函数的特点k=xy为定值,列出方程,求出k的值,便可求出反比例函数的解析式;根据k的值求出B点的坐标,用待定系数法便可求出一次函数的解析式.
(2)根据函数图象可直接解答.
(1)∵AD⊥y轴于点D,OD=3,
∴![]() ,
,
∴AD=2.即A(﹣2,3),
将A点坐标代入y=![]() (k≠0),得k=﹣2×3=﹣6.
(k≠0),得k=﹣2×3=﹣6.
反比例函数的解析式为y=﹣![]() .
.
将B点坐标代入y=﹣![]() 中,得﹣1=﹣
中,得﹣1=﹣![]() ,解得n=6.即B(6,﹣1),
,解得n=6.即B(6,﹣1),
将A、B两点坐标代入y=ax+b,得![]() ,解得
,解得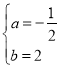 .
.
所以一次函数的解析式为y=﹣![]() x+2.
x+2.
(2)ax+b≥![]() 的自变量x的取值范围是x≤﹣2或0<x≤6.
的自变量x的取值范围是x≤﹣2或0<x≤6.


科目:初中数学 来源: 题型:
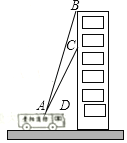
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
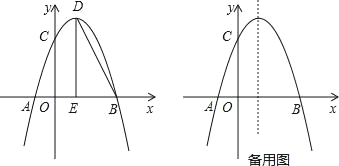
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接DB.
(1)求此抛物线的解析式及顶点D的坐标;
(2)点M是抛物线上的动点,设点M的横坐标为m.
①当∠MBA=∠BDE时,求点M的坐标;
②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
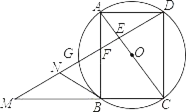
【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB,⊙O及CB延长线交于点F、G、M.
(1)求证:四边形ABCD为矩形;
(2)若N为MF中点,求证:NB是⊙O的切线;
(3)若F为GE中点,且DE=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
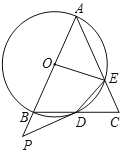
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
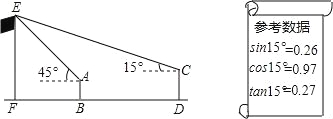
【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com