
分析 由组合数公式可得从5根木棒中任取3根的情况数目,由三角形的三边关系分析可得取出的三根可以搭成钝角三角形的情况数目,由等可能事件的概率公式,计算可得答案.
解答 解:从长度分别为1,2,3,4,5的五条线段中,任取三条,所有的情况共有${C}_{5}^{3}$=10种,
其中,取出的三边能构成钝角三角形时,必须最大边的余弦值小于零,即:较小的两个边的平方和小于第三边的平方,
故满足构成钝角三角形的取法只有:2、3、4 和2、4、5 两种,
故取出的三条线段为边能构成钝角三角形的概率是 $\frac{2}{10}$=$\frac{1}{5}$,
故答案为$\frac{1}{5}$.
点评 本题考查等可能事件计算,涉及三角形三边的关系,关键是分析出可以构成钝角三角形的情况,属于基础题.


科目:初中数学 来源: 题型:解答题
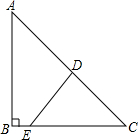 如图所示,某海军基地位于A处,在其正南方向100海里处有一重要目标B,在B的正东方向100海里处也有一重要目标C,小岛D位于AC的中点,岛上有一补给码头,一艘军舰从A出发,经B到C匀速航行,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
如图所示,某海军基地位于A处,在其正南方向100海里处有一重要目标B,在B的正东方向100海里处也有一重要目标C,小岛D位于AC的中点,岛上有一补给码头,一艘军舰从A出发,经B到C匀速航行,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
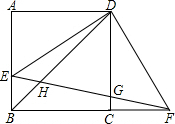 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线交于点F,连接EF与CD交于点G、与对角线BD相交于点H
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线交于点F,连接EF与CD交于点G、与对角线BD相交于点H查看答案和解析>>
科目:初中数学 来源: 题型:解答题
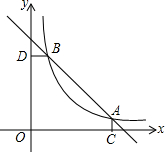 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(3a,2b-9)、B(a,b-2)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(3a,2b-9)、B(a,b-2)两点. 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
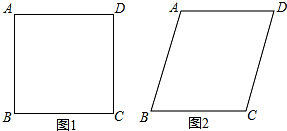 将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,AC=$\sqrt{2}$.
将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,AC=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com