
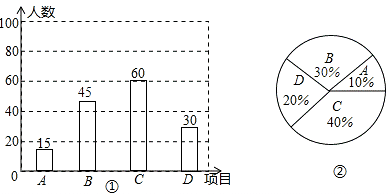
【题目】为推广阳光体育“大课间”活动,某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目,为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: 
(1)在这项调查中,共调查了多少名学生?
(2)请计算喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的4名学生中有2名男生,2名女生.现从这4名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
【答案】
(1)解:15÷10%=150(名),
答;在这项调查中,共调查了150名学生
(2)解:本项调查中喜欢“立定跳远”的学生人数=150﹣15﹣60﹣30=45(人),
它所占百分比= ![]() ×100%=30%,
×100%=30%,
画图如下:
(3)解:画树状图为:
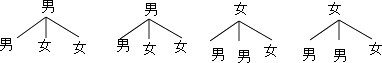
共有12种等可能的结果数,其中相同性别的学生的结果数为4,
所以相同性别的学生的概率= ![]() =
= ![]()
【解析】(1)用A类人数除以它所占百分比即可得到调查的总人数;(2)用总人数分别减去A、C、D类人数即可得到B类人数,再计算B类所占百分比,然后补全统计图;(3)用A表示男生,B表示女生,先画树状图展示所有12种等可能的结果数,再找出到同性别学生的结果数,然后根据概率公式求解.
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在直角坐标系中,有A(0,3),B(2,1),C(﹣3,﹣3)三点.
(1)请在平面直角坐标系中描出各点,并画出三角形ABC;
(2)三角形ABC的面积是 ;(直接写出结果)
(3)设BC交y轴于点P,试求P点的坐标.
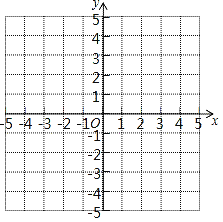
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,过点A作直线EF. 
(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王在解关于x的方程3a-2x=15时,误将-2x看作2x,得方程的解x=3,
(1)求a的值;
(2)求此方程正确的解;
(3)若当y=a时,代数式![]() 的值为5,求当y=-a时,代数式
的值为5,求当y=-a时,代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移3个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1的位置,并写出点A1、B1、C1的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com