练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

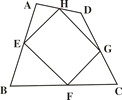
    【题目】如图，已知E、F、G、H是四边形ABCD四边的中点，则四边形EFGH的形状为_____；如四边形ABCD的对角线AC 与BD的和为40，则四边形EFGH的周长为________.

    【答案】平行四边形； 40

    【解析】

    利用三角形的中位线定理求出四边形EFGH的两组对边相等，即可证得四边形EFGH是平行四边形，继而即可求得EFGH的周长．

    解：连接AC、BD，

    ∵E、F、G、H分别为四边形ABCD四边的中点，

    ∴EH=BD，FG=BD，HG=AC，EF=AC，

    ∴EH=FG，EF=HG，

    ∴四边形EFGH是平行四边形．

    ∴四边形EFGH的周长=EH+HG+FG+EF=×2×AC+×2×BD=AC+BD=40．

    故答案为：平行四边形；40．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于．

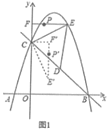
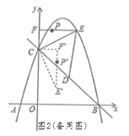
    （1）求函数表达式；

    （2）点是线段中点，点是上方抛物线上一动点，连接，．当的面积最大时，过点作轴垂线，垂足为，点为线段上一动点，将绕点顺时针方向旋转90°，点，，的对应点分别是，，，点从点出发，先沿适当的路径运动到点处，再沿运动到点处，最后沿适当的路径运动到点处停止．求面积的最大值及点经过的最短路径的长；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.

    （1）求证：BE=CF.

    （2）当四边形ACDE为菱形时，求BD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，顶点为的抛物线：()经过点和轴上的点，，．

    （1）求该抛物线的表达式；

    （2）联结，求；

    （3）将抛物线向上平移得到抛物线，抛物线与轴分别交于点(点在点的左侧)，如果与相似，求所有符合条件的抛物线的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在⊙O中，直径MN＝10，正方形ABCD的四个顶点分别在⊙O及半径OM、OP上，并且∠POM＝45°，求正方形的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙Ｏ的直径，点P是AB下方的半圆上不与点A，B重合的一个动点，点C为AP的中点，连接CO并延长，交⊙Ｏ于点D，连接AD，过点D作⊙Ｏ的切线，交PB的延长线于点E，连接CE．

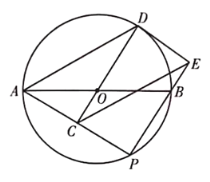
    （1）求证：△DAC≌△ECP；

    （2）填空：

    ①当∠DAP=______°时，四边形DEPC为正方形；

    ②在点 P的运动过程中，若⊙Ｏ的直径为10，tan∠DCE=，则AD=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李辉到服装专卖店去做社会调查，了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法，并获得了如下信息：

    营业员

    嘉琪

    嘉善

    月销售件数/件

    400

    300

    月总收入/元

    7800

    6600

    假设月销售件数为x件，月总收入为y元，销售每件奖励a元，营业员月基本工资为b元．

    （1）求a、b的值．

    （2）若营业员嘉善某月总收入不低于4200元，那么嘉善当月至少要卖多少件衣服？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

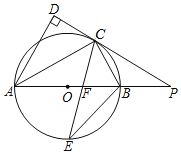
    【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AC平分∠DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为点D，CE平分∠ACB，交AB于点F，交⊙O于点E．

    （1）求证：PC与⊙O相切；

    （2）求证：PC＝PF；

    （3）若AC＝8，tan∠ABC＝，求线段BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明参加班长竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票．如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图．

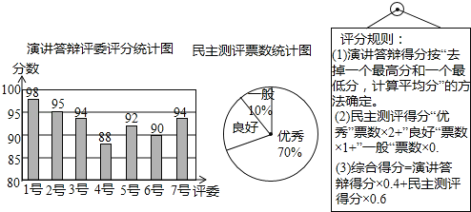
    (1)求评委给小明演讲答辩分数的众数，以及民主测评为“良好”票数的扇形圆心角度数；

    (2)求小明的综合得分是多少？

    (3)在竞选中，小亮的民主测评得分为82分，如果他的综合得分不小于小明的综合得分，他的演讲答辩得分至少要多少分？

    查看答案和解析>>

    同步练习册答案