
【题目】如图,在平面直角坐标系![]() 中,顶点为
中,顶点为![]() 的抛物线
的抛物线![]() :
:![]() (
(![]() )经过点
)经过点![]() 和
和![]() 轴上的点
轴上的点![]() ,
,![]() ,
,![]() .
.
(1)求该抛物线的表达式;
(2)联结![]() ,求
,求![]() ;
;
(3)将抛物线![]() 向上平移得到抛物线
向上平移得到抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() (点
(点![]() 在点
在点![]() 的左侧),如果
的左侧),如果![]() 与
与![]() 相似,求所有符合条件的抛物线
相似,求所有符合条件的抛物线![]() 的表达式.
的表达式.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)抛物线
;(3)抛物线![]() 为:
为:![]() 或
或![]() .
.
【解析】
(1)根据题意,可以写出点B和点A的坐标,从而可以得到该抛物线的表达式;
(2)根据(1)中的函数解析式,可以求得点M的坐标,从而可以求得直线AM的函数解析式,从而可以求得S△AOM;
(3)根据题意,利用分类讨论的方法和三角形相似的知识可以求得点F的坐标,从而可以求得抛物线C2的表达式.
解:(1)过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,
∵![]() ,∴
,∴![]()
∵![]()
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]()
∵抛物线![]() :
:![]() 经过点
经过点![]() ,
,
∴可得: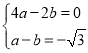 ,
,
解得: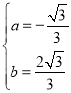
∴这条抛物线的表达式为![]() ;
;
(2)过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,
∵![]() =
=![]()
∴顶点![]() 是
是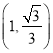 ,得
,得![]()
设直线AM为y=kx+b,
把![]() ,
,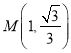 代入得
代入得 ,解得
,解得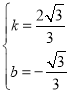
∴直线![]() 为
为![]()
令y=0,解得x=![]()
∴直线![]() 与
与![]() 轴的交点
轴的交点![]() 为
为![]()
∴![]()
(3)∵![]() 、
、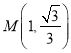 ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .由抛物线的轴对称性得:
.由抛物线的轴对称性得:![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() .
.
∴当![]() 与
与![]() 相似时,有:
相似时,有:![]() 或
或![]()
即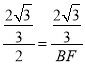 或
或 ,
,
∴![]() 或
或![]() .
.
∴![]() 或
或![]()
设向上平移后的抛物线![]() 为:
为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴抛物线![]() 为:
为:![]()
当![]() 时,
时,![]() ,
,
∴抛物线![]() 为:
为:![]() .
.
综上:抛物线![]() 为:
为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
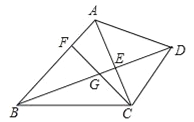
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
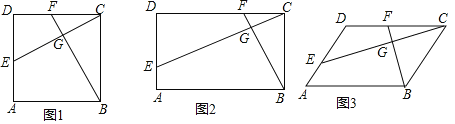
【题目】(1)如图1,正方形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边长的点,
边长的点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图2,矩形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,
边上的点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() .求证:
.求证:![]() ;
;
(3)如图3,若(2)种的四边形![]() 是平行四边形,且
是平行四边形,且![]() ,则
,则![]() 是否仍然成立?若成立,请证明;若不成立,请说明理由.
是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,以A为圆心,弦AB为半径画弧交⊙O于点C,连结BC交AD于点E,若DE=3,BC=8,则⊙O的半径长为( )

A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某兴趣小组用无人机进行航拍测高,无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20米,则2号楼的高度为_____米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
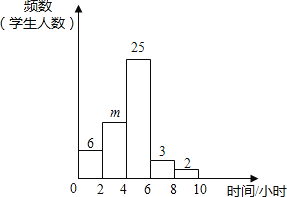
(1)求m的值;
(2)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表或画树状图的方法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
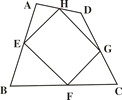
【题目】如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为_____;如四边形ABCD的对角线AC 与BD的和为40,则四边形EFGH的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.有下列结论:①MN=![]() ;②若MN与⊙O相切,则AM=
;②若MN与⊙O相切,则AM=![]() ;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
;③若∠MON=90°,则MN与⊙O相切;④l1和l2的距离为2,其中正确的有( )
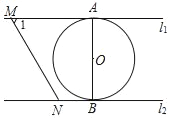
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
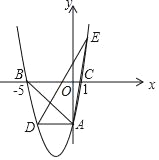
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣5交y轴于点A,交x轴于点B(﹣5,0)和点C(1,0),过点A作AD∥x轴交抛物线于点D.
(1)求此抛物线的表达式;
(2)点E是抛物线上一点,且点E关于x轴的对称点在直线AD上,求△EAD的面积;
(3)若点P是直线AB下方的抛物线上一动点,当点P运动到某一位置时,△ABP的面积最大,求出此时点P的坐标和△ABP的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com