
���� ��1�����¼�AΪ��Ȼ�������¼����ɵ����еĺ;�Ϊż�������ɵ�a��b��cȫΪż����ȫΪ������
��2�����¼�B�����ĸ��ʴ����¼�A�����ĸ��ʣ��ɵ�a��b��c����1������2��ż����2������1��ż����
��� �⣺��1��a��b��cȫΪż����ȫΪ�������ɣ���2��4��6��1��3��5��
��2��a��b��c����1������2��ż����2������1��ż�����ɣ���1��2��4��
����״ͼ�ã�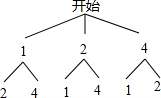
�߹���6�ֵȿ��ܵĽ������Ϊ��������4�������
���¼�B�����ĸ���Ϊ$\frac{2}{3}$��
���� ���⿼�����б�������״ͼ������ʣ��õ���֪ʶ��Ϊ������=������������������֮�ȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
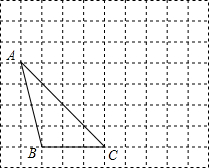 �������������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���ABC�����������λ����ͼ��ʾ������ABC������ƽ��5����λ�á�A1B1C1��������ƽ��2����λ�á�A2B2C2��
�������������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���ABC�����������λ����ͼ��ʾ������ABC������ƽ��5����λ�á�A1B1C1��������ƽ��2����λ�á�A2B2C2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
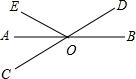 ��ͼ����ֱ֪��AB��CD�ཻ��O�㣬OAƽ�֡�EOC����EOC=60�㣬���BOD=30�㣮
��ͼ����ֱ֪��AB��CD�ཻ��O�㣬OAƽ�֡�EOC����EOC=60�㣬���BOD=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
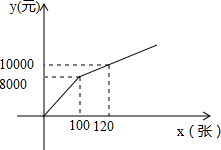 Ϊ�ḻȺ�ڵ�ҵ�������������֯����������������ֲ����λ�����뵥λЭ���Ź�Ʊʱ�Ƴ����ַ������蹺����Ʊ��Ϊx���ţ����ܷ���Ϊy��Ԫ��������һ������λ��������8000Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��50Ԫ�����ܷ���=���������+��Ʊ�ѣ�
Ϊ�ḻȺ�ڵ�ҵ�������������֯����������������ֲ����λ�����뵥λЭ���Ź�Ʊʱ�Ƴ����ַ������蹺����Ʊ��Ϊx���ţ����ܷ���Ϊy��Ԫ��������һ������λ��������8000Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��50Ԫ�����ܷ���=���������+��Ʊ�ѣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com