
����Ŀ��ij����˾ӵ������100������ͳ�ƣ���ÿ�����������Ϊ3000Ԫʱ����ȫ�������ÿ�����������ÿ����50Ԫʱ��δ����ij���������1��������ij�ÿ��ÿ����Ҫά����150Ԫ��δ����ij�ÿ��ÿ����Ҫά����50Ԫ��
��1����ÿ�����������Ϊ3600Ԫʱ�����������������
��2����ÿ���������Ϊ����Ԫʱ������˾�������棨�������۳�ά���ѣ��ɴﵽ306600Ԫ��
���𰸡�
��1���⣺��������ã�100�� ![]() =88��������
=88��������
��ÿ�����������Ϊ3600Ԫʱ�������88����
��2���⣺��ÿ�����������Ϊ��3000+x��Ԫ��
����������100�� ![]() ��[��3000+x����150]��
��[��3000+x����150]�� ![]() ��50=306600��
��50=306600��
��ã�x1=900��x2=1200��
��3000+900=3900��Ԫ����3000+1200=4200��Ԫ����
��ÿ�����������Ϊ3900Ԫ��4200Ԫʱ��������ﵽ306600Ԫ
����������1�����������г���ʽ�����㼴�ɵõ��������2����ÿ�����������Ϊ��3000+x��Ԫ�����������г����̣�������̵Ľ⼴�ɵõ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������8��3��8��6��7��8��7����������λ���ֱ��ǣ� ��
A.8��6
B.7��6
C.7��8
D.8��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��m:y=2x+2��ֱ��n����ƽ��2����λ������ƽ��5����λ�õ��ģ�����2a,7����ֱ��n�ϣ���a=__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
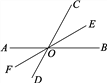
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OEƽ�֡�BOC����BOC��70�㣬OF��OE�ķ����ӳ��ߣ�
(1)���DOF���BOF�Ķ�����
(2)OFƽ�֡�AOD��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����6����ȫһ�����ֱ�д������1��2��3��4��5��6����������һ���������ϵ����֣�Ȼ��Ž�ȥ������һ�����������������ϵ�����֮��Ϊ5�ĸ���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��10��24�������ʱ������Ϊ��ͨ���̽�ġ���������塱�ĸ���Ĵ�����ʽͨ�����������ܳ�Լ55000m���ÿ�ѧ��������ʾ�������ܳ�Ϊ________m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������������ijѧУ��֯ʦ���μ�һ��һ�ȵ�ֲ���̻�������������7���ͳ������мס������ֿͳ������ǵ��ؿ�����������±��������ü��ֿͳ�x������ܷ���ΪyԪ��
���ֿͳ� | ���ֿͳ� | |
�ؿ���/(��/��) | 60 | 40 |
���/(Ԫ/��) | 360 | 300 |
��1�����y����λ��Ԫ����x����λ������֮��ĺ�����ϵʽ��
��2������У����350��ʦ��ǰ���μ��Ͷ������ж������������
��3��������ʦ��ѧУԤ֧�����2400Ԫ������Ԥ֧��������Ƿ���н��ࣿ���н��࣬���ɽ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y=��x+b�������ύ��C��D���㣬ֱ��AB�������ύ��A��B���㣬�߶�OA��OC�ij��Ƿ���x2��3x+2=0����������OA��OC����
��1�����A��C�����ꣻ
��2��ֱ��AB��ֱ��CD���ڵ�E������E���߶�AB���е㣬����������y=![]() ��k��0����ͼ���һ����֧������E����k��ֵ��
��k��0����ͼ���һ����֧������E����k��ֵ��
��3���ڣ�2���������£���M��ֱ��CD�ϣ�����ƽ�����Ƿ���ڵ�N��ʹ�Ե�B��E��M��NΪ������ı��������Σ������ڣ���ֱ��д�����������ĵ�N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�BC��x���غϣ����ӶԽ���BD��y���ڵ�E������A��AG��BD�ڵ�G��ֱ��GF��AD�ڵ�F��AB��OC�ij��ֱ���һԪ���η���x-5x+6=0��������AB��OC������tan��ADB=![]() .
.
��1�����E����G�����ꣻ
��2��ֱ��GF����AGDΪ��AGF����DGF���������Σ���S��AGF��S��DGF =3:1����ֱ��GF�Ľ���ʽ��
��3����P��y���ϣ�������ƽ�����Ƿ����һ��Q��ʹ�Ե�B��D��P��QΪ������ı����Ǿ��Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵������.
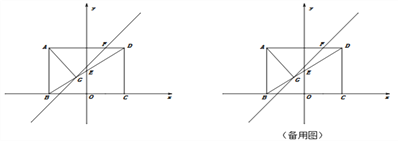
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com