
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=13���ף�BC=10���ף�AD��BC�ڵ�D������P�ӵ�A������ÿ��1�����ٶ����߶�AD�����յ�D�˶����趯���˶�ʱ��Ϊt�룮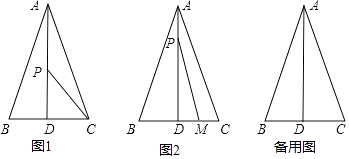
��1����AD�ij���
��2����P��C����ľ���Ϊ ![]() ʱ����t��ֵ��
ʱ����t��ֵ��
��3������M�ӵ�C������ÿ��2�����ٶ�������CB���˶�����M���Pͬʱ�������ҵ���P�˶����յ�Dʱ����MҲֹͣ�˶����Ƿ����ʱ��t��ʹ��S��PMD= ![]() S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
S��ABC�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��AB=AC=13��AD��BC��
��BD=CD=5cm���ҡ�ADB=90�㣬
��AD2=AC2��CD2
��AD=12cm
��2��
�⣺AP=t��
��PD=12��t��
��Rt��PDC�У�PC= ![]() ��CD=5�����ݹ��ɶ����ã�PC2=CD2+PD2��
��CD=5�����ݹ��ɶ����ã�PC2=CD2+PD2��
��29=52+��12��t��2��
��t=10��t=14���ᣩ��
����t��ֵΪ10s
��3��
�⣺�������t��ʹ��S��PMD= ![]() S��ABC��
S��ABC��
��BC=10��AD=12��
��S��ABC= ![]() BC��AD=60��
BC��AD=60��
�� ����M���߶�CD�ϣ�
�� 0��t�� ![]() ʱ��PD=12��t��DM=5��2t��
ʱ��PD=12��t��DM=5��2t��
��S��PMD= ![]() S��ABC��
S��ABC��
�� ![]() ��12��t����5��2t��=
��12��t����5��2t��= ![]() ��
��
2t2��29t+43=0
���t1= ![]() ����ȥ����t2=
����ȥ����t2= ![]()
�� ����M������DB�ϣ��� ![]() ��t��12��
��t��12��
��S��PMD= ![]() S��ABC
S��ABC
�� ![]() ��12��t����2t��5��=
��12��t����2t��5��= ![]() ��
��
2t2��29t+77=0
��� t=11��t= ![]()
���ϣ�����t��ֵΪ ![]() s�� 11s��
s�� 11s�� ![]() s��ʹ��S��PMD=
s��ʹ��S��PMD= ![]() S��ABC
S��ABC
����������1�����ݵ������������ʺ��ɶ�����ɣ���2�����ݹ��ɶ�������������⼴�ɣ���3�����������г�PD��MD�ı���ʽ�ⷽ���飬����M��D���������������ͬ�����Խ��зֶ����ۼ��ɣ�ע��Լ��������
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����20��ײˣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�
��������IJ�ֵ����λ��ǧ�ˣ� |
|
|
|
|
|
|
�� �� | 1 | 4 | 2 | 3 | 2 | 8 |
��1��20��ײ��У����ص�һ��������һ����______ǧ�ˣ�
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ�ˣ�
��3�����ײ�ÿǧ���ۼ�![]() Ԫ���������20��ײ˿�������Ԫ��
Ԫ���������20��ײ˿�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1��x2��x3�ķ���Ϊ4����2 x1+3��2 x2+3��2 x2+3�ķ���Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ij�����һ����ѧ����ɼ����÷�ȡ����������ͳ�Ʒ����������гɼ��ɵ͵��߷ֳ����飬�����Ƴ���ͼ��Ƶ���ֲ�ֱ��ͼ������ֱ��ͼ�ṩ����Ϣ���ش��������⣺ 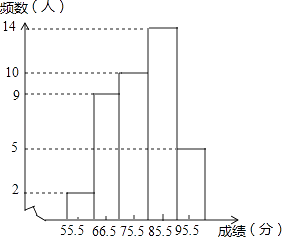
��1���ð����ͬѧ�μ���β��飻
��2����β���ɼ�����λ�������������ڣ�
��3������Уһ����800������ѧ���μ���β��飬�ɼ�80�����ϣ�����80�֣�Ϊ���㣬���Ƹ�У�����ѧ��������������Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��1��19�գ�����ͳ�ƾֹ�����2015���۾������ݣ��������㣬ȫ�����������ֵΪ676000��Ԫ��676000�ÿ�ѧ��������ʾΪ�� ��
A.6.76��106
B.6.76��105
C.67.6��105
D.0.676��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳�����A��B�����ͺż����������ּ������Ľ����۸�ֱ�Ϊÿ̨30Ԫ��40Ԫ���̳�����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ������6̨A�ͺź�3̨B�ͺż��������ɻ�����120Ԫ�����̳�����A��B�����ͺż����������ۼ۸�ֱ��Ƕ���Ԫ��������=���ۼ۸����۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������βٳ��ij��ǿ���2.5����������Ҫ���������������ij��Ϳ����ӳ�20m�����ij��ǿ���2����������ǰ�����βٳ����ܳ���______m��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com