
分析 (1)依据收费可知有20立方米的单价为6.8元每立方米,有4立方米的单价为12元每立方米;
(2)8立方米时,单价为6.8元每立方米,20×6.8=136<196,故乙用户超过20立方米,然后设乙用户用水x立方米,最后根据乙用户应交水费为196元列方程求解即可.
解答 解:(1)20×6.8+(24-20)×12=184元.
答:该用户4月份应交的水费184元.
(2)甲用户应交水费=8×6.8=54.4,
∵20×6.8=136<196,
∴乙用户用水超过20立方米.
设乙用户用水x立方米.
根据题意得:20×6.8+12(x-20)=196.
解得:x=25.
答:甲应交54.4元水费,乙用户用水25立方米.
点评 本题主要考查的是一元一次方程的应用,判断出各用户用水量是否超过20立方米是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 2 | 4 | 2 | 1 |
| A. | 极差是3 | B. | 众数是4 | C. | 中位数40 | D. | 平均数是20.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
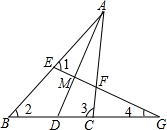 如图,在△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC于点E、M、F,交BC的延长线于点G,给出下列四个等式:①∠1=$\frac{1}{2}$(∠2+∠3);②∠1=$\frac{1}{2}$(∠3-∠2);③∠4=$\frac{1}{2}$(∠3-∠2);④∠4=$\frac{1}{2}$∠1.其中,正确的是①③(填序号).
如图,在△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC于点E、M、F,交BC的延长线于点G,给出下列四个等式:①∠1=$\frac{1}{2}$(∠2+∠3);②∠1=$\frac{1}{2}$(∠3-∠2);③∠4=$\frac{1}{2}$(∠3-∠2);④∠4=$\frac{1}{2}$∠1.其中,正确的是①③(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
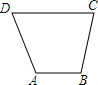 为迎接雨季的到来,某市决定对城边某条泄水沟进行清淤整理,水沟的截面为一梯形,如图所示,为保证泄水量,梯形面积规划为30m2,为了美观,要求AB=$\frac{1}{2}$CD,设AB的长为x m,沟深为y m.
为迎接雨季的到来,某市决定对城边某条泄水沟进行清淤整理,水沟的截面为一梯形,如图所示,为保证泄水量,梯形面积规划为30m2,为了美观,要求AB=$\frac{1}{2}$CD,设AB的长为x m,沟深为y m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com