
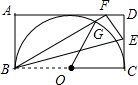
 如图,在矩形ABCD中,BC=12,以BC为直径的半圆O恰好与AD相切,现将矩形ABCD沿BE折叠,使点C落在边AD的点F处,并交半圆O于点G,则扇形OCG的面积为( )
如图,在矩形ABCD中,BC=12,以BC为直径的半圆O恰好与AD相切,现将矩形ABCD沿BE折叠,使点C落在边AD的点F处,并交半圆O于点G,则扇形OCG的面积为( )| A. | 6π | B. | 12π | C. | 24π | D. | 无法确定 |
分析 求出BC=2AB,推出BF=2AB,求出∠AFB=30°,求出∠GOC,即可求出扇形OCG的面积.
解答 解:∵以BC为直径的半圆,正好与对边AD相切,
∴BC=2AB,
∴BF=2AB,
∵∠A=90°,
∴∠AFB=30°,
∴∠OBF=30°,
∵OB=OG,
∴∠OBF=∠OGB=30°,
∴∠GOH=60°,
∴∠DOK=120°,
∴∠AOK=60°,
∴扇形OCG的面积=$\frac{60π×{6}^{2}}{360}$=6π,
故选A.
点评 此题考查了折叠问题,矩形的性质,切线的性质,含30度角的直角三角形性质,扇形的面积,解题时要注意找到对应的等量关系,注意:圆的切线垂直于过切点的半径;在直角三角形中,如果有一条直角边是斜边的一半,那么这条直角边所对的角是30度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,E、F是对角线AC上的两点,∠DEF=∠EFB.
如图,平行四边形ABCD中,E、F是对角线AC上的两点,∠DEF=∠EFB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:
已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某总学全体学生的身体素质情况 | |
| B. | 调查某市中学生压岁钱的使用情况 | |
| C. | 调查某班全体学生的身高 | |
| D. | 调查某品牌烟花爆竹燃放安全的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16×109元 | B. | 1.6×1010元 | C. | 0.16×1011元 | D. | 1.6×109元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com