
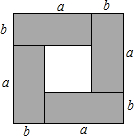
 利用图形的面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
利用图形的面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.分析 (1)利用面积分割法,可求阴影部分面积,各部分用代数式表示即可;
(2)将x-$\frac{1}{x}$=3两边平方可得${x}^{2}+\frac{1}{{x}^{2}}=11$,先将x+$\frac{1}{x}$两边平方可求得其值,再开方根据x>0可得x+$\frac{1}{x}$的值;
(3)利用面积分割法,可构造正方形,使其边长等于a+m=b+n=c+l=k(注意a≠b≠c,m≠n≠l),并且正方形里有边长是a、l;b、m;c、n的长方形,通过画成的图可发现,al+bm+cn<k2.
解答 解:(1)由图可得,4ab=(a+b)2-(a-b)2;
(2)∵x-$\frac{1}{x}$=3(其中x>0),
∴$(x-\frac{1}{x})^{2}={3}^{2}$,
即${x}^{2}-2+\frac{1}{{x}^{2}}=9$,
∴${x}^{2}+\frac{1}{{x}^{2}}=11$,
∴$(x+\frac{1}{x})^{2}={x}^{2}+2+\frac{1}{{x}^{2}}=13$,
∵x>0,
∴$x+\frac{1}{x}=\sqrt{13}$;
(3)构造一个边长为k的正方形,如图所示:显然a+m=b+n=c+l=k,
根据图形可知,正方形内部3个矩形的面积和小于正方形的面积,
故al+bm+cn<k2.
点评 本题主要考查完全平方公式的几何背景及公式间的相互转化,利用几何图形推导代数恒等式,要注意几何图形整体面积与各部分面积的关系.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:填空题
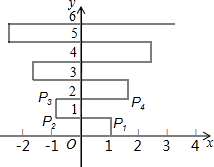 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
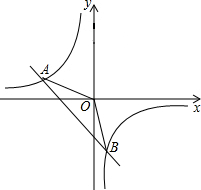 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,-n)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
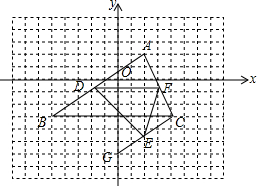 【阅读理解】
【阅读理解】查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com