
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°, 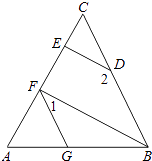
(1)求证;BF∥DE.
(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.
【答案】
(1)证明:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠AFG=∠C.
∵∠1+∠2=180°,∠CDE+∠2=180°,
∴∠1=∠CDE.
∵∠CED=180°﹣∠C﹣∠CDE,∠CFB=180°﹣∠AFD﹣∠1,
∴∠CED=∠CFB,
∴BF∥DE.
(2)解:∵DE⊥AC,BF∥DE,
∴∠AFB=∠AED=90°,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°.
∵∠AFB=∠AFG+∠1=90°,
∴∠AFB=60°.
【解析】(1)根据∠AGF=∠ABC可得出BC∥GF,进而可得出∠AFG=∠C,再根据角的计算可得出∠1=∠CDE,由此即可得出∠CED=∠CFB,根据“同位角相等,两直线平行”即可得出BF∥DE;(2)根据DE⊥AC、BF∥DE即可得出∠AFB=90°,再结合∠1+∠2=180°、∠2=150°以及∠AFB=∠AFG+∠1即可算出∠AFB的度数.


科目:初中数学 来源: 题型:
【题目】2016年“龙岗年货博览会”在大运中心体育馆展销,小丽从家出发前去购物,途中发现忘了带钱,于是打电话让妈妈马上从家里送来,同时小丽也往回走,遇到妈妈后聊了一会儿,接着继续前往大运中心体育馆.设小丽从家出发后所用时间为t,小丽与体育馆的距离为S,下面能反映S与t的函数关系的大致图象是( )
A.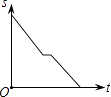
B.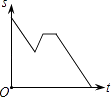
C.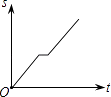
D.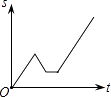
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
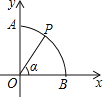
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(+26)+(﹣14)+(﹣16)+(+8)
(2)(﹣5.3)+(﹣3.2)﹣(﹣2.5)﹣(+4.8)
(3)(﹣8)×(﹣25)×(﹣0.02)
(4)( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )×(﹣36)
)×(﹣36)
(5)(﹣1)÷(﹣10 ![]() )÷(﹣1
)÷(﹣1 ![]() )
)
(6)8+(﹣3)2×(﹣2)
(7)0﹣23÷(﹣4)3﹣ ![]()
(8)100÷(﹣2)2﹣(﹣2)÷(﹣ ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通信市场竞争日益激烈,某通信公司的手机市话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com