
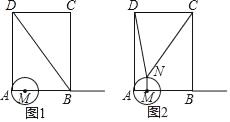
����Ŀ����ͼ1���ھ���ABCD�У�AB=9��BC=12����M�ӵ�A��������ÿ��2����λ���ȵ��ٶ���AB������AB���˶����Ե�MΪԲ�ģ�MA��Ϊ�뾶��Բ����ͼ2������M��NM��AB������M�ڵ�N�����˶�ʱ��Ϊt�룮
��1����գ�BD=�� ����BM=�� ����������ȷ��ֵ��t�Ĵ���ʽ��ʾ��
��2������M��BD����ʱ��
����t��ֵ��
������CDN�������
��3������CNDΪֱ��������ʱ�����t��ֵ��
���𰸡���1��15��9��t����2����t=2��36����3��t=4.5��
��������������(1)������Rt��ABD�Ĺ��ɶ������BD�ij��ȣ�����AM=t�ó�BM�ij��ȣ�(2)�١��жϳ���BME�͡�BDA���ƣ��ó�����ʽ�������̼��ɵó��𰸣��ڡ������MN��CD���ϵĸߣ����������ε������ʽ�ó��𰸣�(3)������N��ֱ��FG��MN���ֱ�AD��BC�ڵ�F��G���ֱ����![]() ��
��![]() ��t�Ĺ�ϵʽ��Ȼ�����DNC=90�����DCN=90������������t��ֵ��
��t�Ĺ�ϵʽ��Ȼ�����DNC=90�����DCN=90������������t��ֵ��
��⣺��1�����ı���ABCD�Ǿ��Σ� ��AD=BC=12����BAD=90�㣬
��Rt��ABD�У�AB=9��BC=12�����ݹ��ɶ����ã�BD=![]() =15��
=15��
���˶�֪��AM=t�� ��BM=AB��AM=9��t��
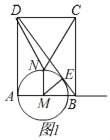
��2������ͼ1����M��BD��E�� ��ME��BD�� ���BEM=��BAD=90�㣬 �ߡ�EBM=��ABD��
���BME�ס�BDA�� ��![]() �� ��
�� ��![]() �� ��t=2��
�� ��t=2��
�ڡ�MN=AM=2t=4�� ��CD���ϵĸ�ΪAD��MN=12��4=8�� ��S��CDN=![]() ��9��8=36��
��9��8=36��
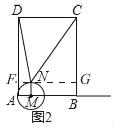
��3����ͼ2������N��ֱ��FG��MN���ֱ�AD��BC�ڵ�F��G��
��FN=2t��GN=9��2t��DF=CG=12��2t�� ��DN2=DF2+FN2=��12��2t��2+��2t��2��
��CN2=CG2+GN2=��12��2t��2+��9��2t��2��
������DNC=90��ʱ��DN2+CN2=CD2�� �ࣨ12��2t��2+��2t��2+��12��2t��2+��9��2t��2=81��
����4t2��33t+72=0�� �ߡ�=����33��2��4��4��72��0�� ���˷�����ʵ������
������DCN=90��ʱ����N��BC�ϣ�BN=BA=2t=9�� ��t=4.5��
����������t=4.5�룮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
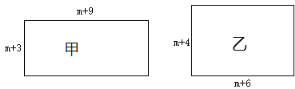
����Ŀ���мס�������������ֽƬ���߳���ͼ��ʾ![]() ,����ֱ�Ϊ
,����ֱ�Ϊ![]() ��
��![]() .
.
��1���ټ��㣺![]() ______,
______,![]() ______��
______��
������<����=������>����գ�![]() ______
______![]()
��2����һ��������ֽƬ���ܳ����ҳ����ε��ܳ���ȣ����Ϊ![]() .
.
�ٸ������εı߳���______(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
��С��ͬѧ���֣�![]() ��
��![]() �IJ���
�IJ���![]() ��.���ж�С���ķ����Ƿ���ȷ����ͨ������˵���������.
��.���ж�С���ķ����Ƿ���ȷ����ͨ������˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��AC��4��BD��16������ABO�ص�A����C�ķ���ƽ�ƣ��õ���A��B��O��������A�����C�غ�ʱ����A���B��֮��ľ���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������Ļ�����ʶ�����������ܼ��ţ���ɫ��������ij�мƻ��ڳ���Ͷ��һ������������������������ΪA��B���ֲ�ͬ���ͣ�����A�ͳ�����400Ԫ��B�ͳ�����320Ԫ��
��1������������������������Ե�Ͷ����ij�����ij�����ʽ������Ͷ��A��B���ֿ��͵ĵ�����100�����ܼ�ֵ36800Ԫ�����ʱ����Ե�Ͷ�ŵ�A�ͳ���B�ͳ�����������
��2���Ե�Ͷ�Ż�õ��˹��������Ͽɣ����о��������������������ȫ���̿��������Ե�Ͷ����A��B�����͵������Ƚ���Ͷ�ţ���Ͷ���ܼ�ֵ������184��Ԫ�����ʳ���10���˿�ƽ��ÿ100����������A�ͳ���B�ͳ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A��B��C�����Ӧ�����ֱ���a��b��7,����![]() ,
,![]() ,PΪ������һ����,��P��A����,��������������ÿ��
,PΪ������һ����,��P��A����,��������������ÿ��![]() ����λ���ȵ��ٶ������˶�,��Q�ӵ�C����������CA�����A�����˶�,��P��Q����ͬʱ������
����λ���ȵ��ٶ������˶�,��Q�ӵ�C����������CA�����A�����˶�,��P��Q����ͬʱ������

��1����a��b��ֵ
��2����P�˶����߶�OB���е�ʱ,��Q�˶���λ��ǡ�����߶�AB������B�����ȷֵ�,���Q���˶��ٶ�
��3����![]() ��������,��P��Q�����ľ�����6����λ����ʱ,��OP�ij���
��������,��P��Q�����ľ�����6����λ����ʱ,��OP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ��������ֽƬ����ֱ�DZ�AB��6��BC��8������ABC�۵���ʹAB����б��AC�ϣ��ۺ�ΪAD����BD�ij�Ϊ(��)

A. 6B. 5C. 4D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ѧ��һ���ı��εĿյ�ABCD������ͼ��ʾ��ѧУ�ƻ��ڿյ�����ֲ��Ƥ����������A=90����AB=3m��BC=12m��CD=13m��DA=4m����ÿƽ���ײ�Ƥ��Ҫ250Ԫ����ѧУ��ҪͶ������ʽ����Ƥ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻУ�Ļ���ijѧУ��������ѧ��Ȥζ�˶��ᣬ��������Ŀȷ��Ϊ�������������ܡ��������������ܺͰκ������֣�Ϊ�˽�ѧ�����������˶���ϲ���������������˸�Уa��ѧ����ϲ����һ����Ŀ��ÿ��ѧ����ѡ��ֻ��ѡ�������е�һ�֣����������������Ƴ���ͼ��������ͳ��ͼ����
ѧ����ϲ���Ļ��Ŀ������ͳ�Ʊ�

����ͼ�����ṩ����Ϣ������������⣺
��1��a= ��b= ��c= ��
��2���뽫����ͳ��ͼ����������
��3�����ݵ�������������Ƹ�У3000��ѧ�����ж�����ѧ����ϲ�������ܣ�
��4�����ݵ�������ij�������������������������ܡ��������������ܺͰκ����ɷֱ��ΪA��B��C��D��E������ѡ�����������ѵ�����û���״ͼ���б��ķ�����ǡ��ѡ��ѧ��ϲ���̶���ߵ�����ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AD��80����B����C�����߶�AD�ϵĵ㣮
��1����ͼ1������MΪAB���е㣬��NΪBD���е㣬���߶�MN�ij���
��2����ͼ2����BC��10����E���߶�AC���е㣬��F���߶�BD���е㣬��EF�ij���
��3����ͼ3����AB��5��BC��10����P��Q�ֱ��B��C�������D�˶����˶��ٶȷֱ�Ϊÿ���ƶ�1����λ��ÿ���ƶ�4����λ���˶�ʱ��Ϊt�룬��EΪAQ���е㣬��FΪPD���е㣬��PE��QF����t��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com