
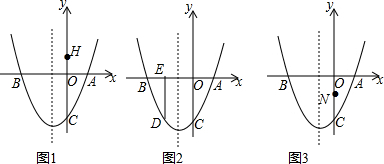
���� ��1����������y=x2+bx+c��x�ύ�ڵ�A��1��0���͵�B����y�ύ�ڵ�C��0��-3�������ô���ϵ����������ö��κ����Ľ���ʽ��
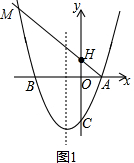
��2����ֱ��AH���������ߵĽ���M��Ϊ����ʱ|MA-MH|��ֵ����ݴ���ϵ�������ֱ��AH�Ľ���ʽ��Ȼ��������߽���ʽ�������̣��ⷽ�̼������M������ꣻ
��3���ҳ�E�����y��ĶԳƵ�E�䣨2��0��������DE�佻y����F����ʱ��EF+DF=E��F+DF=E��D������DE�Ƕ�ֵ�����Դ�ʱ��EDF���ܳ���С�����ݴ���ϵ�������ֱ��DE��Ľ���ʽ��Ȼ����x=0���������F�����ꣻ
��4���ֱ��QN��AC��QN��AC��ƽ��ȥ������ע�������ֱ��QN�Ľ���ʽ�����ݽ������⼴����ô𰸣�С�IJ�Ҫ©�⣻
���  �⣺��1��������ã�$\left\{\begin{array}{l}{a+2+c=0}\\{c=-3}\end{array}\right.$��
�⣺��1��������ã�$\left\{\begin{array}{l}{a+2+c=0}\\{c=-3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=1}\\{c=-3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=x2+2x-3��
��2�����ڣ�
��ͼ1����ֱ��AH���������ߵĽ���M��Ϊ����ʱ|MA-MH|��ֵ���
��ֱ��AH�Ľ���ʽΪy=kx+b��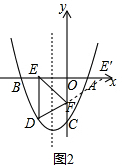
��$\left\{\begin{array}{l}{k+b=0}\\{b=1}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$��
��ֱ��AH�Ľ���ʽΪy=-x+1��
��$\left\{\begin{array}{l}{y=-x+1}\\{y={x}^{2}+2x-3}\end{array}\right.$��$\left\{\begin{array}{l}{x=-4}\\{y=5}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$��
�ߵ�M��y����࣬
��M��-4��5����
��3����ͼ2���ҳ�E�����y��ĶԳƵ�E�䣨2��0����
����DE�佻y����F����ʱ��EF+DF=E��F+DF=E��D��
�ߵ�E��-2��0����ED��AB���������ڵ�D��
��D�ĺ�����Ϊ-2������y=x2+2x-3��y=4-4-3=-3��
��D��-2��-3����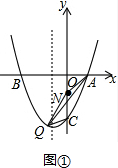
��DE=3�Ƕ�ֵ��
���ʱ��EDF���ܳ���С��
��ֱ��DE��Ľ���ʽΪy=mx+n��
��$\left\{\begin{array}{l}{-2m+n=-3}\\{2m+n=0}\end{array}\right.$�����$\left\{\begin{array}{l}{m=\frac{3}{4}}\\{n=-\frac{3}{2}}\end{array}\right.$��
��y=$\frac{3}{4}$x-$\frac{3}{2}$��
��x=0����y=-$\frac{3}{2}$��
��F��0��-$\frac{3}{2}$����
��4�����ڣ�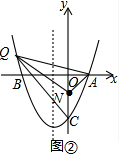
��ͼ�٣���QN��ACʱ����A����C��QN�ľ�����ȣ�
��S��QNC=S��QNA��
��A��1��0����C��0��-3����
��AC�Ľ���ʽΪy=3x-3��
��QN��AC��N��0��-1����
��QN�Ľ���ʽΪy=3x-1��
��$\left\{\begin{array}{l}{y=3x-1}\\{y={x}^{2}+2x-3}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-4}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$��
��Q��-1��-4����
��ͼ�ڣ���QN��AC��ƽ��ʱ��
�ߵ�A��C��ֱ��QN�ľ�����ȣ�
��ֱ��QN���߶�AC���е�M��$\frac{1}{2}$��-$\frac{3}{2}$����
��ֱ��QN�Ľ���ʽΪy=-x-1��
��$\left\{\begin{array}{l}{y=-x-1}\\{y={x}^{2}+2x-3}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{-3+\sqrt{17}}{2}}\\{y=\frac{1-\sqrt{17}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{-3-\sqrt{17}}{2}}\\{y=\frac{1-\sqrt{17}}{2}}\end{array}\right.$��
��Q��-$\frac{3+\sqrt{17}}{2}$��$\frac{1+\sqrt{17}}{2}$����
����ڵ�Q��-$\frac{3+\sqrt{17}}{2}$��$\frac{1+\sqrt{17}}{2}$����-1��-4����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ��ֱ������κ����Ľ��������Լ�������������������֪ʶ�������ۺ��Ժ�ǿ���ѶȽϴ���Ĺؼ���ע�����ν��˼�롢��������˼���뷽��˼���Ӧ��


 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ������£��棩 | 21 | 22 | 25 | 24 | 23 | 26 |
| ���� | 1 | 2 | 4 | 3 | 3 | 2 |
| A�� | 22 | B�� | 23 | C�� | 23.5 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
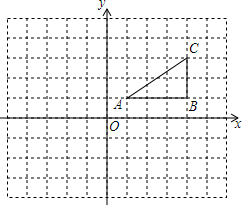 ��ͼ����ƽ��ֱ������ϵ�У�������ÿһ��С�����εı߳�Ϊ1����λ���ȣ���֪��ABC��
��ͼ����ƽ��ֱ������ϵ�У�������ÿһ��С�����εı߳�Ϊ1����λ���ȣ���֪��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
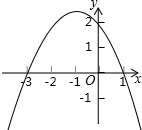 ������y=ax2+bx+c��ͼ����ͼ��ʾ����ʹ��y��0��x��ȡֵ��Χ�ǣ�������
������y=ax2+bx+c��ͼ����ͼ��ʾ����ʹ��y��0��x��ȡֵ��Χ�ǣ�������| A�� | x��2 | B�� | x��-3 | C�� | -3��x��1 | D�� | x��-3��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У���C=90�㣬ADƽ�֡�CAB��BEƽ�֡�CBA��AD��BE�ཻ�ڵ�O������AOB�����ΪS�����ı���ABDE�����Ϊ��������
��ͼ���ڡ�ABC�У���C=90�㣬ADƽ�֡�CAB��BEƽ�֡�CBA��AD��BE�ཻ�ڵ�O������AOB�����ΪS�����ı���ABDE�����Ϊ��������| A�� | 2S | B�� | 1.5S | C�� | 1.2S | D�� | 1.8S |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com