
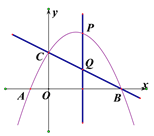
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,һ�κ���y��![]() x��2��ͼ����x�ύ�ڵ�A,��y�ύ�ڵ�C,������y��ax2��bx��c����ֱ��x��
x��2��ͼ����x�ύ�ڵ�A,��y�ύ�ڵ�C,������y��ax2��bx��c����ֱ��x��![]() �Գƣ��Ҿ���A. C���㣬��x�ύ����һ��ΪB.
�Գƣ��Ҿ���A. C���㣬��x�ύ����һ��ΪB.
(1)�������ߵĽ���ʽ��
(2)����PΪֱ��AC�Ϸ����������ϵ�һ��,����P��PQ��x����M����AC��Q����PQ�ġ����ֵ�������ʱ��APC�������
(3)�������ߵĶԳ������ҳ�ʹ��ADCΪֱ�������εĵ�D,ֱ��д����D������.
���𰸡���1��y��![]() x2��
x2��![]() x��2��(2)4����3��D�������Ϊ(
x��2��(2)4����3��D�������Ϊ(![]() ,5)��(
,5)��(![]() ,5)��(
,5)��(![]() ,1��
,1��![]() )��(
)��(![]() ,1��
,1��![]() ).
).
����������������1����ֱ�߹���A���ɵó���A�����꣬��A��B����ֱ��x=![]() �Գƿ��ҳ�B������꣮��ֱ�߾�����C�������C�����꣬���ô���ϵ����������������ߵĽ���ʽ��
�Գƿ��ҳ�B������꣮��ֱ�߾�����C�������C�����꣬���ô���ϵ����������������ߵĽ���ʽ��
��2��ֱ��AC�Ľ���ʽΪy=-![]() x+2����
x+2����![]() x+y-2=0�����Q��������m��-
x+y-2=0�����Q��������m��-![]() m+2������P��������m��-
m+2������P��������m��-![]() m2+
m2+![]() m+2�����ɴ˵õ�PQ=-
m+2�����ɴ˵õ�PQ=-![]() ��m-2��2+2���ɶ��κ�����ֵ���õ�����P��2��3�����ɷָ��ã�S��PAC=S����OCPM+S��PMA-S��AOC��
��m-2��2+2���ɶ��κ�����ֵ���õ�����P��2��3�����ɷָ��ã�S��PAC=S����OCPM+S��PMA-S��AOC��
��3��������ڣ����D�����꣬��ADCΪֱ�������η����������
�ٵ���CΪֱ�Ƕ���ʱ����DM��y����M�ɡ�CD1M�ס�ACO�ɵã�CM=3������OM=5����D1��![]() ��5����
��5����
��ͬ������AΪֱ�Ƕ���ʱ����D2��![]() ��-5����
��-5����
�۵���DΪֱ�Ƕ���ʱ����D3��MN��y�ᣮ�ɡ�CD3M�ס�D3NA�ɵã�n2-2n=![]() ����D3��
����D3��![]() ,1��
,1��![]() ����D4��
����D4��![]() ,1��
,1��![]() ����
����
��⣺(1)��y��![]() x��2��0����ã�x��4��
x��2��0����ã�x��4��
����A������Ϊ(4,0).
��A��B����ֱ��x��![]() �Գƣ� ���B������Ϊ(1,0).
�Գƣ� ���B������Ϊ(1,0).
��x��0����y��2��
���C������Ϊ(0,2)��
��������y��ax2��bx��c������A�� B��C��
���� ��ã� a��
��ã� a��![]() ��b��
��b��![]() ��c��2.
��c��2.
�������߽���ʽΪy��![]() x2��
x2��![]() x��2
x��2
(2)ֱ��AC�Ľ���ʽΪy����![]() x��2,��
x��2,��![]() x��y2��0��
x��y2��0��
���Q������Ϊ(m����![]() m��2) ����P������Ϊ(m,
m��2) ����P������Ϊ(m, ![]() m2��
m2��![]() m��2)��
m��2)��
��PQ����![]() m2��
m2��![]() m��2��������
m��2��������![]() m��2��
m��2��
��![]() m2��2m����
m2��2m����![]() ��m��2��2��2
��m��2��2��2
�൱m��2ʱ��PQ�����2
��ʱ��P��2,3��S��PAC��S����OCPM��S��PMA��S��AOC��5��3��4��4
(3)�������,��D�������Ϊ(![]() ,5)��(
,5)��(![]() ,5)��(
,5)��(![]() ,1��
,1��![]() )��(
)��(![]() ,1��
,1��![]() ).
).
�ⷨ���£���D������꣨![]() ��m��
��m��
��ADCΪֱ�������η����������
�ٵ���CΪֱ�Ƕ���ʱ����DM��y����M
�ɡ�CD1M�ס�ACO�ɵã�![]()
��![]() ,CM��3 ��OM��5��D1��
,CM��3 ��OM��5��D1��![]() ,5��
,5��
��ͬ������AΪֱ�Ƕ���ʱ����D2(![]() ,5)
,5)
�۵���DΪֱ�Ƕ���ʱ:
��D3��MN��y��
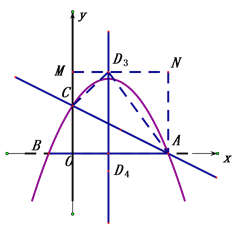
�ɡ�CD3M�ס�D3NA�ɵã�![]()
�� ���ɵã�n2��2n��
���ɵã�n2��2n��![]()
��ã�n��1��![]()
D3(![]() ,1��
,1��![]() ),D4(
),D4(![]() ,1��
,1��![]() )
)
��D�������Ϊ(![]() ,5)��(
,5)��(![]() ,5)��(
,5)��(![]() ,1��
,1��![]() )��(
)��(![]() ,1��
,1��![]() ).
).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��¶¶�����¹�����һ̨����ˮ�������Ե���ˮ���Ĺ���ԭ����������.����˵�����֪������ˮ��������ʾ���¶�Ϊ�ڲ�ˮ����ˮ���¶ȣ�ÿ�μ���ǰ����Ԥ���¶�ֵ��������ˮ���ﵽԤ���¶Ⱥ���ˮ����ֹͣ���ȣ��������¹���.����ʹ�ù����У�����ˮ�����Զ���ˮ��ˮ�»��½�.
¶¶���ֵ���ˮ����ˮ����¶�y����λ���棩���ͨ��Դ���ʱ��x����λ��min��֮����ں�����ϵ��������ˮ���Ŀ��أ�Ԥ���¶�Ϊ70�棬����¼ˮ�±仯��������±��������ڽ�ͨ��Դ��ĵ�8minʱ������ˮ���ﵽԤ���¶ȣ���18minʱ�����迪ʼʹ�õ���ˮ��.
ʱ��x����λ��min�� | 0 | 2 | 4 | 6 | 8 | 18 | 20 | 21 | 25 | 28 |
�¶�y����λ���棩 | 30 | 40 | 50 | 60 | 70 | 70 | 63 | m | 50.4 | 45 |
��1��m��ֵΪ_________��
��2���������������ϵ������ϱ����������ݶ�Ӧ�ĵ㣬����������ĵ㣬������![]() ʱ���¶�y��ʱ��x�仯�ĺ���ͼ��
ʱ���¶�y��ʱ��x�仯�ĺ���ͼ��

��3����¶¶������ʹ�õ���ˮ��ǰ������ˮ�����ڱ��¹��ܵ�ʱ��Ϊ__________min��
��4��δ����ǰ������ˮ����ˮ����ˮ���¶�Ϊ_________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����,��ȷ����( )
A.����ʽ ![]() ��ϵ����-2��������3B.����ʽa��ϵ����0��������0
��ϵ����-2��������3B.����ʽa��ϵ����0��������0
C.![]() ����������ʽ����������1D.����ʽ
����������ʽ����������1D.����ʽ![]() �Ĵ�����2��ϵ��Ϊ
�Ĵ�����2��ϵ��Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڵ�����ֱ�����ཻ��ƽ������λ�ù�ϵ

��1����ͼa����AB��CD����P��AB��CD�ⲿ�����С�B����BOD�������BOD�ǡ�POD����ǣ��ʡ�BOD����BPD+��D���á�BPD����B����D������P�Ƶ�AB��CD�ڲ�����ͼb�����Ͻ����Ƿ��������������˵�����ɣ��������������BPD����B����D֮���к�������ϵ����֤����Ľ��ۣ�
��2����ͼb�У���ֱ��AB�Ƶ�B��ʱ�뷽����תһ���ǶȽ�ֱ��CD�ڵ�Q����ͼc�����BPD����B����D����BQD֮���к�������ϵ��������֤����
��3�����ݣ�2���Ľ�����ͼd�С�A+��B+��C+��D+��E+��F�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A��B�ֱ��ʾ������![]() ��
��![]() ,��A��B�����ľ���ΪAB
,��A��B�����ľ���ΪAB
��1�� ��a=6,b=4,��AB= ����a=-6,b=4,��AB= ��
��2�� ��A��B�����ľ����Ϊ![]() ������
������![]() ��
��![]() ��
��![]() �к�������ϵ��
�к�������ϵ��
��3��д�����з���������������P��ʹ����5��-5�ľ���֮��Ϊ10������������Щ�����ĺ�.
��4��|x-1|+|x+2|ȡ�õ�ֵ��СΪ ��|x-1|-|x+2|ȡ�����ֵΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ��ѧ¥AB����һб�£���֪б��CD�ij�Ϊ12�ף��½Ǧ�Ϊ60�㣬�����йز��ŵĹ涨���Ϧ���39��ʱ�����ܱ��⻬��Σ�գ�ѧУΪ��������ȫ������������б��CD���и��죬�ڱ����½�C����������£�ѧУ����Ҫ���¶�D���ˮƽ�ƶ������ײ��ܱ�֤��ѧ¥�İ�ȫ�������ȡ������
���ο����ݣ�sin39���0.63��cos39���0.78��tan39���0.81��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.24��
��2.24��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ı���ʽΪ
�ı���ʽΪ![]() ��ֱ��
��ֱ��![]() ��x�ύ�ڵ�D��ֱ��
��x�ύ�ڵ�D��ֱ��![]() ��
��![]() ��x�ύ�ڵ�A���Ҿ�����B��ֱ��
��x�ύ�ڵ�A���Ҿ�����B��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
��1����m��ֵ��
��2����ֱ��![]() �ı���ʽ��
�ı���ʽ��
��3������ͼ��ֱ��д��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֵĵ���ά��Ҫ��30ǧ��Զ�Ľ������е������ޣ�����������Ħ�г����ߣ�15���Ӻ�����װ����������ϳ������������ͬʱ�����֪�������ٶ���Ħ�г���1.5�����������ֳ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�һ���ϴ�A�����������A��B��C��D��A��ѭ�����У�����A�������Ϊ��2����2����B�������Ϊ����2����2����C�������Ϊ����2��6����D�������Ϊ��2��6��������������2018����λʱ����������λ�õ�����Ϊ��������

A. ����2��0��B. ��4����2��C. ����2��4��D. ��0����2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com