
【题目】下列说法中,正确的是( )
A.单项式 ![]() 的系数是-2,次数是3B.单项式a的系数是0,次数是0
的系数是-2,次数是3B.单项式a的系数是0,次数是0
C.![]() 是三次三项式,常数项是1D.单项式
是三次三项式,常数项是1D.单项式![]() 的次数是2,系数为
的次数是2,系数为![]()
【答案】D
【解析】
根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
解:A、单项式![]() 的系数是-
的系数是-![]() ,次数是3,系数包括分母,错误;
,次数是3,系数包括分母,错误;
B、单项式a的系数是1,次数是1,当系数和次数是1时,可以省去不写,错误;
C、-3x2y+4x-1是三次三项式,常数项是-1,每一项都包括这项前面的符号,错误;
D、单项式-![]() 的次数是2,系数为-
的次数是2,系数为-![]() ,符合单项式系数、次数的定义,正确;
,符合单项式系数、次数的定义,正确;
故选D.
考查的知识点为:单项式中的数字因数叫做这个单项式的系数.单项式中,所有字母的指数和叫做这个单项式的次数;多项式里次数最高项的次数叫做这个多项式的次数.单独的一个字母的系数和次数都是1.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1,以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2,再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3,…,依次进行下去,则点B6的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△APB的面积等于四边形的一半,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一副三角板按如图所示的方式放置,则下列结论正确的是( )

A.∠1=∠2B.如果∠2=30°,则有AC∥DE
C.如果∠2=45°,则有∠4=∠DD.如果∠2=50°,则有BC∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来,![]() ,于是可用
,于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的相反数.
的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
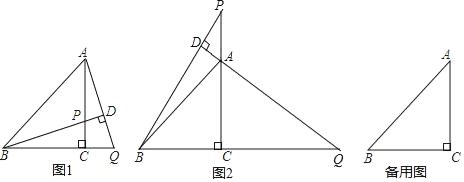
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
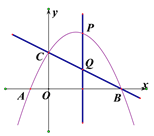
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+2的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=
x+2的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=![]() 对称,且经过A. C两点,与x轴交于另一点为B.
对称,且经过A. C两点,与x轴交于另一点为B.
(1)求抛物线的解析式;
(2)若点P为直线AC上方的抛物线上的一点,过点P作PQ⊥x轴于M,交AC于Q,求PQ的⊥最大值,并求此时△APC的面积;
(3)在抛物线的对称轴上找出使△ADC为直角三角形的点D,直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:如图1是二环三角形,可得S=∠A1+∠A2+…+∠A6=360°
理由:连接A1A4
∵∠1+∠2+∠A1OA4=180°
∠A5+∠A6+∠A5OA6=180°
又∵∠A1OA4=∠A5OA6
∴∠1+∠2=∠A5+∠A6
∴∠A2+∠3+∠1+∠2+∠4+∠A3=360°
∴∠A2+∠3+∠A5+∠A6+∠4+∠A3=360°
即S=360°
(2)延伸探究:

①如图2是二环四边形,可得S=∠A1+∠A2+…+∠A8=720°,请你加以证明
②如图3是二环五边形,可得S= ,聪明的你,能根据以上的规律直接写出二环n边形(n≥3的整数)中,S= 度.(用含n的代数式表示最后的结果)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com