
(1)��ͼ1��ֽƬ��ABCD�У�AD=5,S��ABCD=15,����A��AE��BC,����ΪE,��AE���¡�ABE,����ƽ������DCE�� ��λ�ã�ƴ���ı���AEE��D,���ı���AEE��D����״Ϊ�� ��
A.ƽ���ı��� B.���� C.���� D.������
(2)��ͼ2����(1)�е��ı���ֽƬAEE��D��,��EE����ȡһ��F,ʹEF=4�����¡�AEF������ƽ������DE��F�� ��λ�ã�ƴ���ı���AFF��D.
�� ��֤�ı���AFF��D�����Σ�
�� ���ı���AFF��D�����Խ��ߵij�.
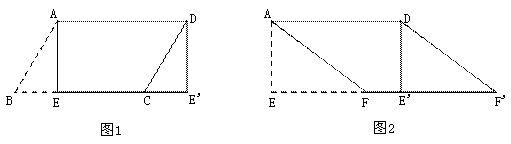
.������(1) ��ƽ��֪��AE DE��, ���ı���AEE��D��ƽ���ı��Σ���AE��BC, ���AEE��=90��,
DE��, ���ı���AEE��D��ƽ���ı��Σ���AE��BC, ���AEE��=90��,
���ı���AEE��D�Ǿ��Σ���Cѡ����ȷ.
(2) �� ��AF DF��, ���ı���AFF��D��ƽ���ı��Σ���AE=3, EF=4 ,��E=90��, ��AF=5,
DF��, ���ı���AFF��D��ƽ���ı��Σ���AE=3, EF=4 ,��E=90��, ��AF=5,
��S��ABCD=AD·AE=15, ��AD=5 , ��AD=AF , ���ı���AFF��D������.
�� ����ͼ�� ����AF��, DF ��
��Rt��AEF���� AE=3, EF��=9, ��AF��=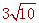
��Rt��DFE���� FE��=1, DE��=AE=3, ��DF=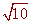
���ı���AFF��D�����Խ��ߵij��ֱ���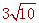 ��
��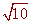 .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������ �Ķ���ΪM����
�Ķ���ΪM���� �ύ�ڵ�A��B����
�ύ�ڵ�A��B���� �ύ�ڵ�C.
�ύ�ڵ�C.
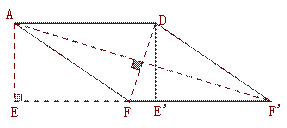
��1����ͼ����֪��A��B������ֱ�Ϊ����1��0������3��0����
��ֱ��д�������ߵı���ʽ�� ��
������BC��BM�����CBM������ֵ��
�۵�D��E�����߶�AB�ϣ���AD=AC���� F���߶�BC�ϣ�����߶�EF��ֱ��
CD��ֱƽ�֣�����DF���� ��ֵ.
��ֵ.
��2���� <0ʱ�������A��B��C�����Բ��
<0ʱ�������A��B��C�����Բ�� �����һ������ΪP����֤����PΪ
�����һ������ΪP����֤����PΪ
���㣬��������ö�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
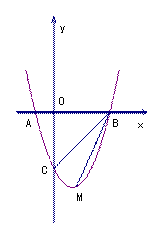
��ͼ�ǡ���ˬ��ͼ������ABH����BCG����CDF�͡�DAE���ĸ�ȫ�ȵ�ֱ�������Σ��ı���ABCD��EFGH���������Σ����AB��10��EF��2���� ôAH������������
ôAH������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
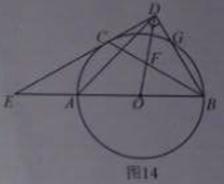
25.��ͼ14��AB�ǡѣϵ�ֱ����C��G�ǡѣ������㣬��AC = CG,����C��ֱ��CD BG�ڵ�D����BA���ӳ����ڵ�E������BC����OD�ڵ�F.
BG�ڵ�D����BA���ӳ����ڵ�E������BC����OD�ڵ�F.
(1)��֤��CD�ǡѣϵ�����.
(2)��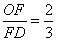 ,��
,�� E�Ķ���.
E�Ķ���.
(3)����AD���ڣ�2���������£���CD=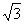 ����AD�ij�.
����AD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
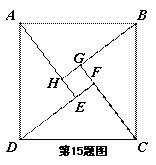
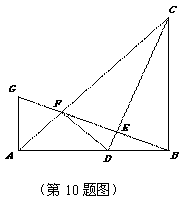
��ͼ����Rt��ABC�У���ABC=90�㣬AB=BC����D���߶�AB�ϵ�һ�㣬����CD������B��BG��CD���ֱ�CD��CA�ڵ�E��F�������A�Ҵ�ֱ��AB��ֱ���ཻ�ڵ�G������DF�����������ĸ����ۣ���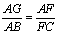 ��������D��AB���е㣬��AF=
��������D��AB���е㣬��AF=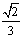 AB���۵�B��C��F��D�ĵ���ͬһ��Բ��ʱ��DF=DB������
AB���۵�B��C��F��D�ĵ���ͬһ��Բ��ʱ��DF=DB������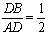 ����
����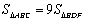 ��������ȷ�Ľ�������ǣ� ��
��������ȷ�Ľ�������ǣ� ��
A���٢� B���ۢ� C���٢ڢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com