练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

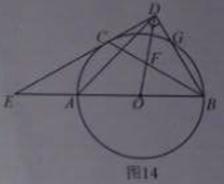
    25.如图14，AB是⊙Ｏ的直径，C、G是⊙Ｏ上两点，且AC = CG,过点C的直线CD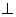BG于点D，交BA的延长线于点E，连接BC，交OD于点F.

    (1)求证：CD是⊙Ｏ的切线.

    (2)若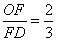,求E的度数.

    (3)连接AD，在（2）的条件下，若CD=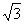，求AD的长.

     


    （1）先证OC//BD即可OC垂直于CD,即为切线

        （2）30

         (3)

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列等式中，正确的是

    A、    B、   C、       D、

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


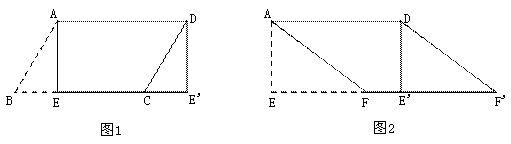
    (1)如图1，纸片□ABCD中，AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′ 的位置，拼成四边形AEE′D,则四边形AEE′D的形状为（     ）

          A.平行四边形          B.菱形          C.矩形          D.正方形

       (2)如图2，在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4，剪下△AEF，将它平移至△DE′F′ 的位置，拼成四边形AFF′D.

          ① 求证四边形AFF′D是菱形；

          ② 求四边形AFF′D两条对角线的长.

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    因式分解：　　　　　　．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    使有意义的x的取值范围是(       )

    A.  x ≠ 1      B.  x ≥ 1      C.  x ＞ 1      D.  x ≥ 0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小丽近6个月的手机话费（单位：元）分别为：18，24，37，28，24，26，这组数据的中位数是       元。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形OABC中，OA=3，OC=5,分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y=(k ＞ 0)的图像经过点D且与边BA交于点E，连接DE.

    （1）       连接OE，若△EOA的面积为2，则k=       ；

    （2）       连接CA、DE与CA是否平行？请说明理由；

    （3）       是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，直线y =－x＋2与反比例函数的图象有唯一公共点. 若直线与反比例函数的图象有2个公共点，则b的取值范围是

    (A)  b﹥2.        (B) －2﹤b﹤2.  (C)  b﹥2或b﹤－2.   (D)  b﹤－2.

     


    查看答案和解析>>

    同步练习册答案