
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P���������¶������ǵ�P��x��ľ���Ϊ![]() ����y��ľ���Ϊ
����y��ľ���Ϊ![]() ����
����![]() �����
�����![]() ��P������������
��P������������![]() �����
�����![]() ��P����������
��P����������
��������P��![]() ��
�� ![]() ������x��ľ���Ϊ4����y��ľ���Ϊ3����Ϊ3��4�����Ե�P��������Ϊ
������x��ľ���Ϊ4����y��ľ���Ϊ3����Ϊ3��4�����Ե�P��������Ϊ![]() .
.
��1���ٵ�A��2�� ![]() ����������Ϊ________��
����������Ϊ________��
������B��![]() ��
�� ![]() ����������Ϊ
����������Ϊ![]() ����
����![]() ��ֵΪ________��
��ֵΪ________��
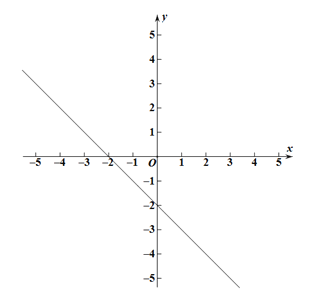
��2������C��ֱ��![]() �����ҵ�C��������Ϊ
�����ҵ�C��������Ϊ![]() �����C��������
�����C��������
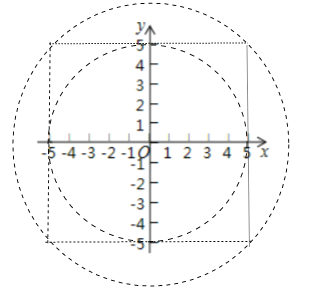
��3������O��������M��ʹ��M��������Ϊ![]() ��ֱ��д����O�İ뾶r��ȡֵ��Χ��
��ֱ��д����O�İ뾶r��ȡֵ��Χ��

���𰸡���1����5������5����2����C��![]() ��
�� ![]() ������
������![]() ��
�� ![]() ������3��
������3��![]() .
.
�������������������1����ֱ�Ӹ��������������Ķ��壬����С����Ϊ������������
����B��a��2����x��ľ���Ϊ2����������������Ϊ5������a=��5��
��2�����ݵ�C������������Ϊ5���ɵ�x=��5��y=��5������ɵý����
��3����ͼ���۲�ͼ���֪������O��ֱ��x=5��ֱ��x=��5��ֱ��y=5��ֱ��y=��5�н���ʱ����O�ϴ��ڵ�M��ʹ��M��������Ϊ5��
����������⣺��1���١���A��2����5����x��ľ���Ϊ5����y��ľ���Ϊ2����2��5������A������������Ϊ5��
�ڡ���B��a��2��������������Ϊ5����a=��5���ʴ�Ϊ��5����5��
��2�����C�����꣨x��y��������C������������Ϊ5����x=��5��y=��5����x=5ʱ��y=��7����x=��5ʱ��y=3����y=5ʱ��x=��7����y=��5ʱ��x=3������C����5��3����3����5����
��3����ͼ���۲�ͼ���֪������O��ֱ��x=5��ֱ��x=��5��ֱ��y=5��ֱ��y=��5�н���ʱ����O�ϴ��ڵ�M��ʹ��M��������Ϊ5����5��r��![]() ��
��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������
ѧϰ��������ȫ�ȵ��ж�����������SAS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ������������������������ߺ�����һ�ߵĶԽǶ�Ӧ����������ν����о���
������˼����
���Dz����������÷������Ա�ʾΪ������ABC����DEF�У�AC=DF��BC=EF����B=��E��Ȼ����B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ�����������������̽����

������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
��1����ͼ��������ABC����DEF��AC=DF��BC=EF����B=��E=90�������� ������֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��2����ͼ��������ABC����DEF��AC=DF��BC=EF����B=��E������B����E���Ƕ۽ǣ���֤����ABC�ա�DEF��
���������������B�����ʱ����ABC����DEF��һ��ȫ�ȣ�
��3������ABC����DEF��AC=DF��BC=EF����B=��E������B����E������ǣ������ó߹���ͼ����������DEF��ʹ��DEF����ABC��ȫ�ȣ�����д������������ͼ�ۼ���
��4����B��Ҫ����ʲô�������Ϳ���ʹ��ABC�ա�DEF����ֱ��д�����ۣ�����ABC����DEF�У�AC=DF��BC=EF����B=��E������B����E������ǣ��� ������ABC�ա�DEF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ּܷ��豸�ڿ��ҵ���е��ռ�������ּ�Ч�ʴ����ߣ�ʹ��ijƷ�����ּܷ��豸��ÿ��ÿСʱ�ּ�Ŀ�����Ǵ�ͳ�ּ�ʽ��25�����������ԣ���5���ô��豸�ּ�8000�������ʱ�䣬��20���ô�ͳ��ʽ�ּ�ͬ�������Ŀ����ʡ4Сʱ��ij�����תվƽ��ÿ����Ҫ�ּ�10�����������ʹ�ô����ּܷ��豸��ÿ��ֻ��Ҫ���Ŷ��������˾Ϳ�����ɷּ�����ÿ�칤��ʱ��Ϊ8Сʱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ѧϰ�����ľ������Ժ���![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽���������벹��������
��1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧ��ֵ���±���

����m=__________��
��2����ͼ����ƽ��ֱ������ϵxOy������������ϱ��и����ӦֵΪ����ĵ�����������ĵ��������ú�����ͼ����
��3���۲캯��ͼ����д��һ���ú�����������
��4����һ��̽������ͼ������
������![]() �и�������ȵ�ʵ������
�и�������ȵ�ʵ������
������������x1��y1������x2��y2���ڴ˺���ͼ��������x2��x1��2ʱ���Ƚ�y1��y2�Ĵ�С��ϵΪ��
y1________y2 �����������������=������
��������x�ķ���![]() ��4��������ȵ�ʵ��������a��ȡֵ��Χ��________��
��4��������ȵ�ʵ��������a��ȡֵ��Χ��________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �����������϶�Ӧ�����ֱ�Ϊ
�����������϶�Ӧ�����ֱ�Ϊ![]() ���ҵ�A�ڵ�B����࣬
���ҵ�A�ڵ�B����࣬![]()
(1)���a��b��ֵ��
(2)����һֻ����P�ӵ�A��������ÿ��3����λ���ȵ��ٶ������˶���ͬʱ��һֻ����Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ������˶�.
����ֻ���Ͼ����ʱ��������
������ֻ�����������ϵĵ�C�����������C��Ӧ������
�۾����ʱ�䣬��ֻ���������������20����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD����AB=3��BC=6��PΪBC����һ�㣬��APDΪ���������Σ�
��1��С��������һ��������������APD������PA=PD����ͼ1��ʾ����tan ![]() ��ֵΪ ��
��ֵΪ ��
��2��������ͼ2���ٻ���һ��������������APD����С���IJ�ͬ���������ʱtan ![]() ��ֵ��
��ֵ��
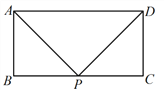

ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��PΪ��ABC�ڲ�����ϵĵ㣬��������PAB����PBC����PAC������һ������������ABC���ƣ���P������ABC�����غϣ�����Ƶ�PΪ��ABC�������Ƶ㣮

���磺��ͼ1����P����ABC���ڲ�����PBC=��A����PCB=��ABC�����BCP�ס�ABC���ʵ�PΪ��ABC�������Ƶ㣮
��ƽ��ֱ������ϵxOy�У�
��1����A����Ϊ(![]() ��
�� ![]() )�� AB��x����B�㣬��E(2��1)��F (
)�� AB��x����B�㣬��E(2��1)��F (![]() ��
�� ![]() )��G (
)��G (![]() ��
�� ![]() )�����������У���������AOB�������Ƶ���� ������ĸ����
)�����������У���������AOB�������Ƶ���� ������ĸ����
��2������M������C�� ![]() ��
��![]() ��
�� ![]() ���ϵ�һ�����㣬NΪx����������һ�����㣻
���ϵ�һ�����㣬NΪx����������һ�����㣻
 ͼ2
ͼ2
�� ��ͼ2�� ![]() ��M�������Ϊ3����NM = NO������P�ǡ�MON�������Ƶ㣬���P�����ꣻ
��M�������Ϊ3����NM = NO������P�ǡ�MON�������Ƶ㣬���P�����ꣻ
����![]() ����NΪ(2��0)������MON�������Ƶ���2����������C���������������ĵ�M���� ��������ͼ3�л�����Щ�㣨������Ҫ�Ļ�ͼ�ۼ�����
����NΪ(2��0)������MON�������Ƶ���2����������C���������������ĵ�M���� ��������ͼ3�л�����Щ�㣨������Ҫ�Ļ�ͼ�ۼ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������һ������,���������:
(1)��֪����![]() ��һԪһ�η���
��һԪһ�η���![]() ���������,���������ϱ�ע
���������,���������ϱ�ע![]() ��
��![]() ��Ӧ�ĵ�,�ֱ����A��B��
��Ӧ�ĵ�,�ֱ����A��B��
(2)��(1)��������,������������һ��C��Ӧ����Ϊ![]() C��A�ľ�����C��B�ľ����5��,��C�ڱ�ʾ5�ĵ�����.
C��A�ľ�����C��B�ľ����5��,��C�ڱ�ʾ5�ĵ�����.
(3)����(1)��(2)�ṩ��������ͼ�٣�����һԪһ�η��̵�֪ʶ����ͼ���е�9������������ǡ������,ʹÿһ�С�ÿһ�С�ÿ��б�Խ��ߵ����ĺ����,Ҫ��:�г����̡��������,��ͼ��.
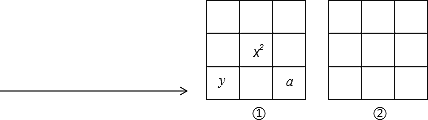
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɱ߳�Ϊ1��С��������ɵ�����С��Ķ���и�㣬�������������������ͬ��ʵ���ϸ�ȡһ����㣬ʹ�����������㲻��ͬһʵ���ϣ��õ������ABC��
��1��AC= ����ABC�� ������
��2����������������������и�����һ�����ֱ�������Σ�ʹ�����������㲻��ͬһʵ���ϣ��������������е������λ���ȫ�ȣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com