
【题目】定义:点P为△ABC内部或边上的点,若满足△PAB,△PBC,△PAC至少有一个三角形与△ABC相似(点P不与△ABC顶点重合),则称点P为△ABC的自相似点.

例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
在平面直角坐标系xOy中,
(1)点A坐标为(![]() ,
, ![]() ), AB⊥x轴于B点,在E(2,1),F (
), AB⊥x轴于B点,在E(2,1),F (![]() ,
, ![]() ),G (
),G (![]() ,
, ![]() ),这三个点中,其中是△AOB的自相似点的是 (填字母);
),这三个点中,其中是△AOB的自相似点的是 (填字母);
(2)若点M是曲线C: ![]() (
(![]() ,
, ![]() )上的一个动点,N为x轴正半轴上一个动点;
)上的一个动点,N为x轴正半轴上一个动点;
 图2
图2
① 如图2, ![]() ,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
,M点横坐标为3,且NM = NO,若点P是△MON的自相似点,求点P的坐标;
②若![]() ,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).
,点N为(2,0),且△MON的自相似点有2个,则曲线C上满足这样条件的点M共有 个,请在图3中画出这些点(保留必要的画图痕迹).

【答案】(1)F,G(2)①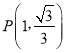 或
或 ②4
②4
【解析】试题分析:(1)如图,连接OF、OE、GB、FB,作GM⊥OB于M,FN⊥OB于N.只要证明△OBG∽△OAB,可得点G是自相似点,△FOB∽△BAO,可得点F是自相似点.
(2)①如图1,过点M作MH⊥x轴于H点.将M的横坐标代入反比例函数解析式求出点M的坐标和OM的长,进而求出直线OM的解析式.在Rt△MHN中,根据勾股定理求出ON=MN=m=2.如图2, ![]() ∽
∽![]() ,过点
,过点![]() 作
作![]() ⊥x轴于Q点,由相似的性质得出
⊥x轴于Q点,由相似的性质得出![]() ,
, ![]() .得出P1的横坐标为1,代入OM解析式求出即可求出P1的坐标;如图3,
.得出P1的横坐标为1,代入OM解析式求出即可求出P1的坐标;如图3, ![]() ,根据相似三角形的性质求出P2N的长,进而可得P2的坐标.
,根据相似三角形的性质求出P2N的长,进而可得P2的坐标.
②以O为圆心2为半径作圆交反比例函数于M1,M2,以N为圆心2为半径作圆交反比例函数的图象于M3,M4.满足条件的点M有4个.
试题解析:
解:(1)如图中,连接OF、OE、GB、FB,作GM⊥OB于M,FN⊥OB于N.
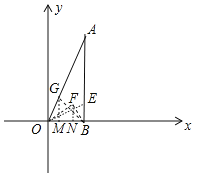
由题意可知点G在OA上,
∵tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=60°,
∵tan∠GBM=![]() =
=![]() =
=![]() ,
,
∴∠OBG=30°,
∴∠BOG=∠AOB,∠OBG=∠A,
∴△OBG∽△OAB,
∴点G是自相似点,
同理可得∠FON=∠A=30°,∠FBO=∠AOB=60°,
∴△FOB∽△BAO,
∴点F是自相似点,
span>故答案为F,G;
(2)①如图1,过点M作MH⊥x轴于H点.
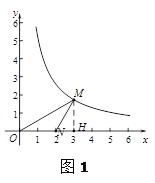
∵M点的横坐标为3,
∴![]() .
.
∴![]() .
.
∴![]() ,直线OM的表达式为
,直线OM的表达式为![]() .
.
∵MH⊥x轴,
∴在Rt△MHN中, ![]() °,
°,![]() .
.
设NM=NO=m,则![]() .
.
∴![]() .
.
∴ON=MN=m=2.
如图2, ![]() ∽
∽![]() ,过点
,过点![]() 作
作![]() ⊥x轴于Q点,
⊥x轴于Q点,

∴![]() ,
, ![]() .
.
∵![]() 的横坐标为1,
的横坐标为1,
∴![]() .
.
∴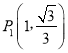 .
.
如图3, ![]() ,
,

∴![]() .
.
∴![]() .
.
∵![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() .
.
∴![]() .
.
∴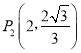 .
.
综上所述, 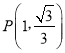 或
或 .
.
②以O为圆心2为半径作圆交反比例函数于M1,M2,以N为圆心2为半径作圆交反比例函数的图象于M3,M4.满足条件的点M有4个.
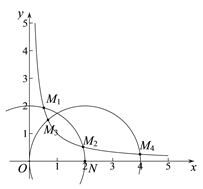
故答案为4.


科目:初中数学 来源: 题型:
【题目】给出下列四个关于是否成反比例的命题,判断它们的真假.
(1)面积一定的等腰三角形的底边长和底边上的高成反比例;
(2)面积一定的菱形的两条对角线长成反比例;
(3)面积一定的矩形的两条对角线长成反比例;
(4)面积一定的直角三角形的两直角边长成比例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为![]() ,到y轴的距离为
,到y轴的距离为![]() ,若
,若![]() ,则称
,则称![]() 为点P的最大距离;若
为点P的最大距离;若![]() ,则称
,则称![]() 为点P的最大距离.
为点P的最大距离.
例如:点P(![]() ,
, ![]() )到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3<4,所以点P的最大距离为![]() .
.
(1)①点A(2, ![]() )的最大距离为________;
)的最大距离为________;
②若点B(![]() ,
, ![]() )的最大距离为
)的最大距离为![]() ,则
,则![]() 的值为________;
的值为________;
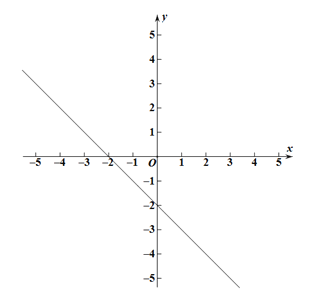
(2)若点C在直线![]() 上,且点C的最大距离为
上,且点C的最大距离为![]() ,求点C的坐标;
,求点C的坐标;
(3)若⊙O上存在点M,使点M的最大距离为![]() ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的性质.
的性质.
(1)先从简单情况开始探究:
① 当函数为![]() 时,
时, ![]() 随
随![]() 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);
② 当函数为![]() 时,它的图象与直线
时,它的图象与直线![]() 的交点坐标为 ;
的交点坐标为 ;
(2)当函数为![]() 时,
时,
下表为其y与x的几组对应值.
x | … |
| 0 | 1 |
| 2 |
| 3 | 4 |
| … |
y | … |
|
| 1 |
| 2 |
| 3 | 7 |
| … |

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A型、B型、C型三种不同的纸板,其中A型:边长为a厘米的正方形;B型:长为a厘米,宽为1厘米的长方形;C型:边长为1厘米的正方形.

(1)A型2块,B型4块,C型4块,此时纸板的总面积为 平方厘米;
①从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形,这个大正方形的边长为 厘米;
②从这10块纸板中拿掉2块同类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形,请问拿掉的是2块哪种类型的纸板?(计算说明)
(2)A型12块,B型12块,C型4块,从这28块纸板中拿掉1块纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出三个相同形状的大正方形,则大正方形的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-11)+(+8) (2)![]()
(3)(+3.5)-(-2.3) -(-2.9) (4)![]()
(5)(-7)-(-4)+(+5)-(-9)
(6)1![]() +(-6.5)+3
+(-6.5)+3![]() +(-1.75)+2
+(-1.75)+2![]() ;
;
(7)![]()
(8)1-3+5-7+9-11+…+97-99
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com