【题目】如图，在楼房MN前有两棵树与楼房在同一直线上，且垂直于地面，为了测量树AB、CD的高度，小明爬到楼房顶部M处，光线恰好可以经过树CD的顶站C点到达树AB的底部B点，俯角为45°，此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点，与地面的夹角为30°，树CD的影长DN为15米，请求出树AB、CD的高度．（结果保留根号）
科目：初中数学 来源： 题型：
【题目】随着智能分拣设备在快递业务中的普及，快件分拣效率大幅提高．使用某品牌智能分拣设备，每人每小时分拣的快件量是传统分拣方式的25倍，经过测试，由5人用此设备分拣8000件快件的时间，比20人用传统方式分拣同样数量的快件节省4小时．某快递中转站平均每天需要分拣10万件快件，如果使用此智能分拣设备，每天只需要安排多少名工人就可以完成分拣工作（每天工作时间为8小时）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：点P为△ABC内部或边上的点，若满足△PAB，△PBC，△PAC至少有一个三角形与△ABC相似（点P不与△ABC顶点重合），则称点P为△ABC的自相似点．
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P为△ABC的自相似点．
在平面直角坐标系xOy中，
（1）点A坐标为(
， 
)， AB⊥x轴于B点，在E(2，1)，F (
， 
)，G (
， 
)，这三个点中，其中是△AOB的自相似点的是 （填字母）；
（2）若点M是曲线C： 
（
， 
）上的一个动点，N为x轴正半轴上一个动点；
图2
① 如图2， 
，M点横坐标为3，且NM = NO，若点P是△MON的自相似点，求点P的坐标；
②若
，点N为(2，0)，且△MON的自相似点有2个，则曲线C上满足这样条件的点M共有 个，请在图3中画出这些点（保留必要的画图痕迹）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明设计了一个问题,分三步完成:
(1)已知关于
的一元一次方程
请完成数轴,并在数轴上标注
与
对应的点,分别记作A、B；
(2)在(1)的条件下,在数轴上另有一点C对应的数为
C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧.
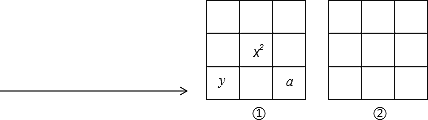
(3)请结合(1)、(2)提供的条件和图①，利用一元一次方程的知识，在图②中的9个方格内填上恰当的数,使每一行、每一列、每条斜对角线的数的和相等,要求:列出方程、并填表格,即图②.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知长方形纸片ABCD，AB=4，BC=10，M是BC的中点，点P沿折线BA—AD运动，以MD为折瘪将长方形纸片向右翻折，使点B落在长方形的AD边上，则折痕MP的长______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）先化简，再求值5x2-[2xy-3（
xy+2）+4x2]，其中x=-2，y=
（2）若（2a-1）2+|2a+b|=0，且|c-1|=2，求c（a3-b）的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是由边长为1的小正方形组成的网格，小格的顶点叫格点，在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一实线上，得到格点△ABC．
（1）AC= ：△ABC是 三角形；
（2）请在下面的正方形网格中各画出一个格点直角三角形，使其中任意两点不在同一实线上，并且三个网格中的三角形互不全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AD＝4，对角线AC与BD交于点O，OE⊥AC交BC于点E，CE＝3，则矩形ABCD的面积为（ ）
A.
B.
C.12D.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
