
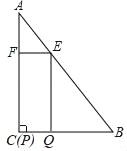
����Ŀ����ͼ���ڡ�ABC�У���A��30�㣬��C��90�㣬AB��12���ı���EFPQ�Ǿ��Σ���P���C�غϣ���Q��E��F�ֱ���BC��AB��AC�ϣ���E���A����B�����غϣ���
��1����AE��8ʱ����EF�ij���
��2����AE��x������EFPQ�����Ϊy��
����y��x�ĺ�����ϵʽ��
����xΪ��ֵʱ��y�����ֵ�����ֵ�Ƕ��٣�
��3��������EFPQ��������ʱ��������EFPQ��ÿ��1����λ���ٶ�������CB���������˶�������P�����Bʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFPQ���ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
���𰸡���1��4����2����y=��![]() x2+3
x2+3![]() x��0��x��12������x=6ʱ��y�����ֵΪ9
x��0��x��12������x=6ʱ��y�����ֵΪ9![]() ����3��S=
����3��S=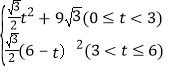
��������
(1)��EF��BC,�ɵ�![]() ,�ɴ˼��ɽ������;
,�ɴ˼��ɽ������;
(2)���ȸ��ݵ�EΪAB��һ��ó��Ա���x��ȡֵ��Χ,����30�ȵ�ֱ�������ε��������EF��AF�ij�,����Rt��ACB��,�������Ǻ������AC�ij�,����FC�ij�,���þ��ε������ʽ�����S�ĺ�����ϵʽ;
�ڰѶ��κ����Ĺ�ϵʽ�䷽���Եý���;
(3)���������ηֱ���⼴�ɽ������.
�⣺��1����Rt��ABC�У���AB=12����A=30�㣬
��BC=![]() AB=6��AC=
AB=6��AC=![]() BC=6
BC=6![]() ��
��
���ı���EFPQ�Ǿ��Σ�
��EF��BC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��EF=4��
��2���١�AB=12��AE=x����E���A����B�����غϣ�
��0��x��12��
���ı���CDEF�Ǿ��Σ�
��EF��BC����CFE=90�㣬
���AFE=90�㣬
��Rt��AFE�У���A=30�㣬
��EF=![]() x��
x��
AF=cos30��AE=![]() x��
x��
��Rt��ACB��AB=12��
��cos30��=![]() ��
��
��AC=12��![]() =6
=6![]() ��
��
��FC=AC��AF=6![]() ��
��![]() x��
x��
��y=FCEF=![]() x��6
x��6![]() ��
��![]() x��=��
x��=��![]() x2+3
x2+3![]() x��0��x��12����
x��0��x��12����
��y=![]() x��12��x��=��
x��12��x��=��![]() ��x��6��2+9
��x��6��2+9![]() ��
��
��x=6ʱ��S�����ֵΪ9![]() ��
��
��3���ٵ�0��t��3ʱ����ͼ1�У��ص������������MFPQN��
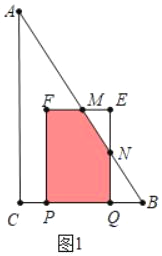
S=S����EFPQ��S��EMN=9![]() ��
��![]() t2=��
t2=��![]() t2+9
t2+9![]() ��
��
�ڵ�3��t��6ʱ���ص������ǡ�PBN��
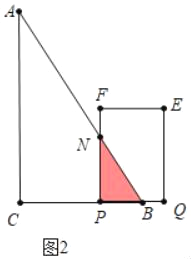
S=![]() ��6��t��2��
��6��t��2��
����������S=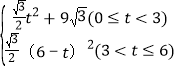



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
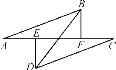
����Ŀ����ͼ����A��E��F��C��һ��ֱ���ϣ�������DEC�ı�EC��AC����ƽ�ƣ�ƽ�ƹ�����ʼ����������������AE��CF��DE��AC�ڵ�E��BF��AC�ڵ�F����AB��CD.��E��F���غ�ʱ��BD��EF�Ĺ�ϵ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����a��0ʱ����![]() ��ֵ����д�������̣�
��ֵ����д�������̣�
��2����a��0��b��0����![]() +
+![]() =0����
=0����![]() ��ֵΪ�� ����
��ֵΪ�� ����
��3����ab��0����![]() +
+![]() +
+![]() ��ֵΪ�� ����
��ֵΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
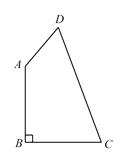
����Ŀ����ͼ�����ı���ABCD�У���B=90�㣬AB=BC=2��AD=1��CD=3��
��1�����DAB�Ķ�����
��2�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ھ���ABCD�У�M��N�ֱ��DZ�AD��BC���е㣬E��F�ֱ����߶�BM��CM���е�
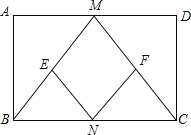
��1����֤����ABM�ա�DCM
��2���ж��ı���MENF��ʲô�����ı��Σ���֤����Ľ��ۣ�
��3����AD��AB= _ʱ���ı���MENF�������Σ�ֻд���ۣ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪OA��OB��OC��OD��AD��BC�ཻ�ڵ�E����ͼ�й���ȫ�������εĶ�����������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��D��BC���е㣬AC�Ĵ�ֱƽ���߷ֱ�AC��AD��AB�ڵ�E��O��F����ͼ��ȫ�ȵ������εĶ�����______ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ�㲥����������ơ�������������ʡĿǰ��ߵ��˹�������Ҳ�Ǹ���������������ȥ����ij�Ƽ���ȤС���������˻����ز��������������������ĸ߶ȣ���֪��ͼ�����˻����ھ��롰������ˮƽ����138�ĵ�C����������˻��Ϲ۲����������ǡΪ30�㣬�۲����������ĵ�ĸ���ǡΪ45�㣮�������ĸ߶ȣ���ע�� ![]() ��1.73���������������
��1.73���������������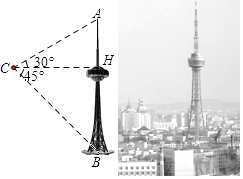
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BE���������ߣ���S��EDC��S��ABC=�� ��
A.1��2
B.1��4
C.1��3
D.2��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com