
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.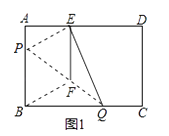
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;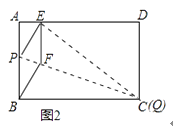
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
【答案】
(1)
证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EF∥AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形
(2)
解:①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,
∴CE=BC=5cm,
在Rt△CDE中,DE= ![]() =4cm,
=4cm,
∴AE=AD﹣DE=5cm﹣4cm=1cm;
在Rt△APE中,AE=1,AP=3﹣PB=3﹣PE,
∴EP2=12+(3﹣EP)2,
解得:EP= ![]() cm,
cm,
∴菱形BFEP的边长为 ![]() cm;
cm;
②当点Q与点C重合时,如图2:
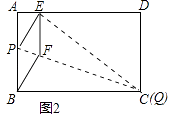
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
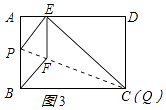
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm
【解析】(1)由折叠的性质得出PB=PE,BF=EF,∠BPF=∠EPF,由平行线的性质得出∠BPF=∠EFP,证出∠EPF=∠EFP,得出EP=EF,因此BP=BF=EF=EP,即可得出结论;(2)①由矩形的性质得出BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,由对称的性质得出CE=BC=5cm,在Rt△CDE中,由勾股定理求出DE=4cm,得出AE=AD﹣DE=1cm;在Rt△APE中,由勾股定理得出方程,解方程得出EP= ![]() cm即可;②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.
cm即可;②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1cm;当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,即可得出答案.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.
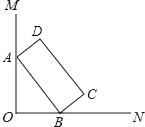
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论. 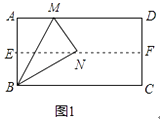
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论. 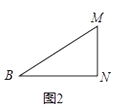
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
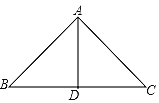
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E. 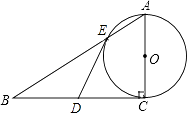
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
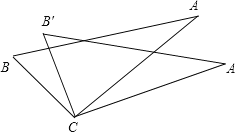
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是以原点为圆心,2 ![]() 为半径的圆,点P是直线上y=﹣x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
为半径的圆,点P是直线上y=﹣x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( ) 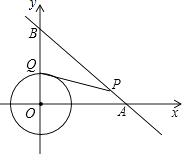
A.4
B.2 ![]()
C.8﹣2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣2xy2)23x2y÷(﹣x3y4)
(2)(2x+y)(2x﹣3)﹣2y(x﹣1)
(3)3(m+1)2﹣5(m+1)(m﹣1)+2(m﹣1)2
(4)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为 . 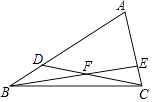
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com