
【题目】如图,正方形ABCD的边长为1cm,AC是对角线,AE平分∠BAC,EF⊥AC于F. 
(1)求证:BE=EF.
(2)求tan∠EAF的值.
【答案】
(1)证明:∵在正方形ABCD中,EF⊥AC,AB⊥BC,
∴∠AFE=∠ABE=90°;
∵AE平分∠BAC,
∴∠BAE=∠FAE;
又∵AE=AE,
∴Rt△BAE≌Rt△FAE,
故AB=AF,BE=FE
(2)解:∵正方形ABCD,
∴在Rt△CEF中,∠ECF=45°,
故FE=CF,
∴BE=CF,
∵正方形ABCD的边长为1 cm,对角线AC= ![]() cm,
cm,
由(1)可得,BE=EF=CF=AC﹣AF=AC﹣AB= ![]() ﹣1(cm),
﹣1(cm),
∴ ![]()
【解析】(1)根据角平分线上的点到角两边的距离相等,可得BE=EF;(2)根据勾股定理,计算正方形的对角线的长,减去AF的长求得CF的长,最后计算tan∠EAF的值.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】学习成为商城人的时尚,义乌市新图书馆的启用,吸引了大批读者.有关部门统计了2011年10月至2012年3月期间到市图书馆的读者的职业分布情况,统计图如下: 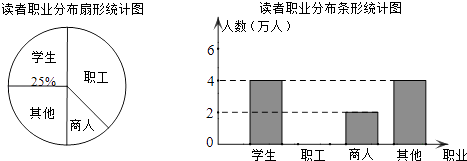
(1)在统计的这段时间内,共有万人到市图书馆阅读,其中商人所占百分比是 ,
(2)将条形统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(3)若今年4月到市图书馆的读者共28000名,估计其中约有多少名职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则能够正确反映y与x之间的函数关系的图象是( )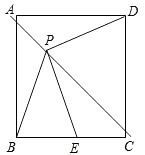
A.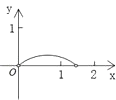
B.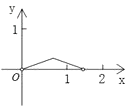
C.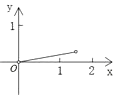
D.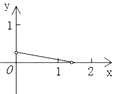
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.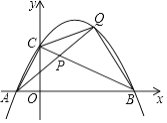
(1)①写出点A,B,C的坐标:A(),B(),C();
②求证:△ABC是直角三角形;
(2)记△BCQ的面积为S,求S关于x的函数表达式;
(3)在点P的运动过程中, ![]() 是否存在最大值?若存在,求出
是否存在最大值?若存在,求出 ![]() 的最大值及点Q的坐标;若不存在,请说明理由.
的最大值及点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( ) 
A.15°
B.20°
C.25°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com