
����Ŀ������ͼ�α任���Գơ�ƽ�ƻ���ת��������и��⣺
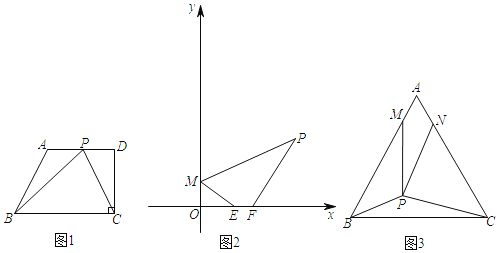
��1����ͼ1�����ı���ABCD�У�AD��BC��CD��BC����ABC��60����AD��8��BC��12����P�DZ�AD�ϵ�����һ�㣬����BPC�ܳ�����СֵΪ�� ��
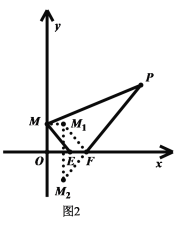
��2����ͼ2����֪M��0��1����P��2+![]() ��3����E��a��0����F��a+1��0������aΪ��ֵʱ���ı���PMEF���ܳ���С��
��3����E��a��0����F��a+1��0������aΪ��ֵʱ���ı���PMEF���ܳ���С��
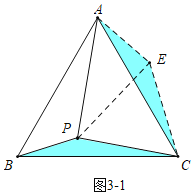
��3����ͼ3��PΪ�ȱ���ABC��һ�㣬��PB��2��PC��3����BPC��150����M��NΪ��AB��AC�ϵĶ��㣬��AM��AN����ֱ��д��PM+PN����Сֵ��
���𰸡���1��![]() ����2��a��
����2��a��![]() ʱ���ı���PMEF�ܳ���С����3��PM+PN����СֵΪ
ʱ���ı���PMEF�ܳ���С����3��PM+PN����СֵΪ![]() ��
��
��������
��1����ͼ1�������������ȸ�����ԳƵ����ʡ�����֮���߶���̵ó�![]() �ܳ���Сʱ����P��λ�ã��ٸ��ݾ��ε����ʡ�ֱ�������ε��������CD�ij����Ӷ��ɵ�
�ܳ���Сʱ����P��λ�ã��ٸ��ݾ��ε����ʡ�ֱ�������ε��������CD�ij����Ӷ��ɵ�![]() �ij���Ȼ�����ù��ɶ����ɵ�
�ij���Ȼ�����ù��ɶ����ɵ�![]() �ij����ɴ˼��ɵó��𰸣�
�ij����ɴ˼��ɵó��𰸣�
��2����ͼ2������������Ҫʹ�ı���PMEF���ܳ���С��ֻ��![]() ��С��������ƽ�ơ���ԳƵ����ʵó�
��С��������ƽ�ơ���ԳƵ����ʵó�![]() ���ٸ�������֮���߶���̵ó�
���ٸ�������֮���߶���̵ó�![]() ��Сʱ����F��λ�ã�Ȼ�����ô���ϵ�������ֱ��
��Сʱ����F��λ�ã�Ȼ�����ô���ϵ�������ֱ��![]() �Ľ���ʽ���Ӷ��ɵ�a��ֵ��
�Ľ���ʽ���Ӷ��ɵ�a��ֵ��
��3����ͼ�������������Ƚ�![]() �Ƶ�C˳ʱ����ת
�Ƶ�C˳ʱ����ת![]() ��������ת�����ʡ����ɶ������PA�ij����ٽ�
��������ת�����ʡ����ɶ������PA�ij����ٽ�![]() �Ƶ�A��ʱ����ת
�Ƶ�A��ʱ����ת![]() ��������ת�����ʡ�����֮���߶����ȷ��
��������ת�����ʡ�����֮���߶����ȷ��![]() ��Сʱ����N��λ�ã�Ȼ����ݵȱ������ε����ʼ��ɵó��𰸣�
��Сʱ����N��λ�ã�Ȼ����ݵȱ������ε����ʼ��ɵó��𰸣�
��1����ͼ1������C����ֱ��AD�ĶԳƵ�![]() ������
������![]() ��AD��
��AD��![]() ����
����![]()
����ԳƵ����ʡ�����֮���߶���̿�֪����ʱ![]() �ܳ���С����СֵΪ
�ܳ���С����СֵΪ![]()
��![]() ��H
��H
![]()
![]()
![]()
���ı���ADCH�Ǿ���
![]()
![]()
![]()
��![]() ��
�У�![]()
![]()
![]()
![]()
![]()
��![]() �ܳ�����СֵΪ
�ܳ�����СֵΪ![]()
�ʴ�Ϊ��![]() ��
��
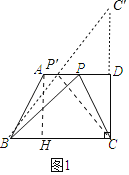
��2���ı���PMEF���������У�PM��EF���ȹ̶�����ֻҪ![]() ��С���ı���PMEF���ܳ���ȡ����Сֵ
��С���ı���PMEF���ܳ���ȡ����Сֵ
��ͼ2������M����ƽ��1����λ���ȣ�EF�ij��ȣ�������![]()
��![]() ���ı���
���ı���![]() ��ƽ���ı���
��ƽ���ı���
![]()
����![]() ����x��ĶԳƵ�
����x��ĶԳƵ�![]() ������
������![]()
��![]() ��
��![]()
![]()
������֮���߶���̵ã�����![]() ����ʱ��
����ʱ��![]() ��С����СֵΪ
��С����СֵΪ![]()
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
����![]() �����
�����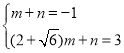
���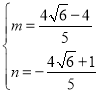
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]()
����![]() �����
�����![]()
���![]()
�ʵ�![]() ʱ���ı���PMEF�ܳ���С��
ʱ���ı���PMEF�ܳ���С��
��3����ͼ3��1�У���![]() �Ƶ�C˳ʱ����ת
�Ƶ�C˳ʱ����ת![]() �õ�
�õ�![]() ������PE
������PE
����ת�����ʵã�![]()
![]() �ǵȱ�������
�ǵȱ�������
![]()
![]()
![]()
��ͼ3��2�У���![]() �Ƶ�A��ʱ����ת
�Ƶ�A��ʱ����ת![]() �õ�
�õ�![]() ������PF����AC�ڵ�D
������PF����AC�ڵ�D
����ת�����ʵã�![]()
![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]()
![]()
������֮���߶���̵ã�����N���D�غ�ʱ��![]() ��С����СֵΪPF
��С����СֵΪPF
��![]() ����СֵΪ
����СֵΪ![]() ��
��


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵꾭��һ�ֽ�������֪���ֽ�����ijɱ���Ϊÿ��20Ԫ���г����鷢�֣����ֽ�����ÿ���������y�����������۵���x��Ԫ�������¹�ϵ��y=��20x+80��20��x��40���������ֽ�����ÿ�����������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ��
��2�����ֽ��������۵��۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3�������۲��Ź涨���ֽ���������۵��۲�����28Ԫ�����̵��������ֽ�����ÿ��Ҫ���150Ԫ�������������۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
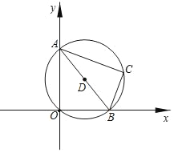
����Ŀ����ͼ������ABC�У���BAC=90�㣬AB=AC=2����ABΪֱ����Բ��BC��D����ͼ����Ӱ���ֵ����Ϊ��������

A. 1 B. 2 C. 1+![]() D. 2��
D. 2��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ����Ϊ10���߶�AB����˵�A����B�ֱ���y�ᡢx���ϻ�������CΪ��ABΪֱ������D��һ�㣨Cʼ���ڵ�һ���ޣ�����tan��BAC=![]() ����A��A0��0��10��������O��0��0����B��O��0��0��������B0��10��0���Ĺ����У���C�˶���·����Ϊ_____��
����A��A0��0��10��������O��0��0����B��O��0��0��������B0��10��0���Ĺ����У���C�˶���·����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��![]() x��1�ֱ�x�ᡢy���ڵ�A��B���ڵڶ���������һ�߳�Ϊ2��������CDEF����֪C����1��1����������P��C������ÿ��1����λ���ٶ�����������CDEF�ı���ʱ���˶�һ�ܣ�����C���ֹͣ�˶�������P���˶���ʱ��Ϊt�룮
x��1�ֱ�x�ᡢy���ڵ�A��B���ڵڶ���������һ�߳�Ϊ2��������CDEF����֪C����1��1����������P��C������ÿ��1����λ���ٶ�����������CDEF�ı���ʱ���˶�һ�ܣ�����C���ֹͣ�˶�������P���˶���ʱ��Ϊt�룮
��1���Ƿ����t��ʹ����PΪԲ�ģ�![]() Ϊ�뾶��Բ��ֱ��AB���У������ڣ��������t��ֵ�������ڣ���˵�����ɣ�
Ϊ�뾶��Բ��ֱ��AB���У������ڣ��������t��ֵ�������ڣ���˵�����ɣ�
��2���ڵ�P�˶���ͬʱ��ֱ��AB��ÿ��1����λ���ٶ������������˶������Pͬʱֹͣ���Ƿ����t��ʹ����PΪԲ�ģ�![]() Ϊ�뾶��Բ��ƽ�ƺ��ֱ��A��B�����У���ֱ��д������t��ֵ��
Ϊ�뾶��Բ��ƽ�ƺ��ֱ��A��B�����У���ֱ��д������t��ֵ��
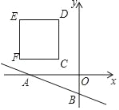
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����Ϊ12cm����Ϊ5cm����Ϊ8cm�ij����壬һֻ֩���һ��������е�A���ų�����������е�����Bȥ�����ϣ���ʱ֩�����е���̾����ǣ� ��
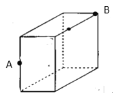
A.13 cmB.15 cmC.21 cmD.25cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̨����һ����Ȼ�ֺ���������̨������ΪԲ�ģ�һ������Ϊ�뾶��Բ���������γɼ��������м�ǿ���ƻ�������ͼ��������ļ�һ̨�������ؼ���B�����A���ڵ�ֱ���ɶ������ƶ�����֪��CΪһ���ۣ��ҵ�C��A�� B����ľ���ֱ�Ϊ300km�� 400km���ҡ�ACB=90��������C��CE��AB�ڵ�E����̨������ΪԲ�ģ��뾶Ϊ260km��Բ��������Ϊ��Ӱ������
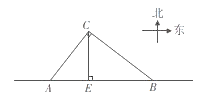
��1�������A�����B֮��ľ��룻
��2�����жϺ���C�Ƿ���ܴ˴�̨���Ӱ�죬��˵�����ɣ�
��3����̨����ٶ�Ϊ25km/h����̨��Ӱ��ú��۶ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������ABC�ı߳�Ϊ4��AD��BC���ϵ�������F��AD���ϵĶ�����E��AC����һ������AE��2����EF��CFȡ����Сֵʱ����ECF�Ķ���Ϊ( )

A. 20�� B. 25�� C. 30�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2014��������籭������ǰϦ��ij������Ʒ�깺��һ������Ϊ40Ԫ����������������60Ԫ���ۣ���ôһ�����ڿ��۳�240�ף��������۾��飬������۵��ۻᵼ���������ļ��٣������۵���ÿ���5Ԫ����������Ӧ����20�ף������۵���Ϊx(120��x��60)Ԫ��������Ϊy�ף�
(1)���y��x�ĺ�����ϵʽ��
(2)�����۵���Ϊ����Ԫʱ�������۶�Ϊ14000Ԫ�����¹�ӯ������Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com