
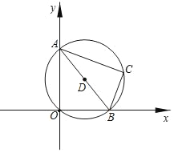
【题目】如图,在平面直角坐标系中,有一条长为10的线段AB,其端点A、点B分别在y轴、x轴上滑动,点C为以AB为直径的⊙D上一点(C始终在第一象限),且tan∠BAC=![]() .则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为_____.
.则当点A从A0(0,10)滑动到O(0,0),B从O(0,0)滑动到B0(10,0)的过程中,点C运动的路径长为_____.
科目:初中数学 来源: 题型:
【题目】从﹣3、﹣2、﹣1、1、2、3这六个数中,随机抽取一个数记作a,使关于x的分式方程![]() 有整数解,且使直线y=3x+8a﹣17不经过第二象限,则符合条件的所有a的和是( )
有整数解,且使直线y=3x+8a﹣17不经过第二象限,则符合条件的所有a的和是( )
A.﹣4B.﹣1C.0D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下列证明过程中的推理根据:
已知:如图所示,AC,BD相交于O,DF平分∠CDO与AC相交于F,BE平分于∠ABO与AC相交于E,∠A=∠C.求证:∠1=∠2.
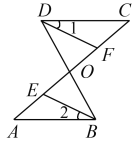
证明:∵∠A=∠C(________),
∴AB∥CD (__________________________________),
∴∠ABO=∠CDO (__________________________________),
又∵∠1=![]() CDO,∠2=
CDO,∠2=![]() ∠ABO (__________________________________),
∠ABO (__________________________________),
∴∠1=∠2(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浚县古城是闻名遐迩的历史文化名城,“元旦”期间相关部门对到浚县观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),根据图中的信息,下列结论错误的是( )
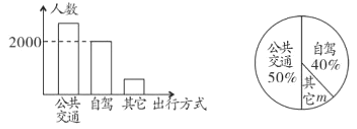
A.此次调查的总人数为5000人
B.扇形图中的![]() 为10%
为10%
C.样本中选择公共交通出行的有2500人
D.若“元旦”期间到浚县观光的游客有5万人,则选择自驾方式出行的有2.5万人
查看答案和解析>>
科目:初中数学 来源: 题型:
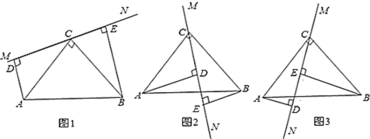
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .易得
.易得![]() (不需要证明).
(不需要证明).
(1)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时
旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)当直线![]() 绕点
绕点![]() 旋转到图3的位置时,其余条件不变,请直接写出此时
旋转到图3的位置时,其余条件不变,请直接写出此时![]() 之间的数量关系(不需要证明).
之间的数量关系(不需要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A(1,﹣![]() ),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
),点B(﹣2,n)在抛物线y=ax2(a≠0)上.
(1)求a的值与点B的坐标;
(2)将抛物线y=ax2(a≠0)平移,记平移后点A的对应点为A′,点B的对应点为B',若四边形ABB′A′为正方形,求平移后的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请用图形变换(对称、平移或旋转)解决下列各题:
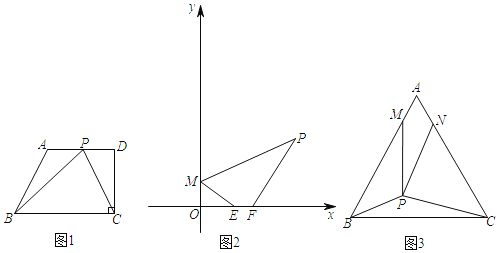
(1)如图1,在四边形ABCD中,AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12,若P是边AD上的任意一点,则△BPC周长的最小值为 .
(2)如图2,已知M(0,1)、P(2+![]() ,3)、E(a,0)、F(a+1,0),问a为何值时,四边形PMEF的周长最小?
,3)、E(a,0)、F(a+1,0),问a为何值时,四边形PMEF的周长最小?
(3)如图3,P为等边△ABC内一点,且PB=2,PC=3,∠BPC=150°,M、N为边AB、AC上的动点,且AM=AN,请直接写出PM+PN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中(如图),抛物线y=ax2-4与x轴的负半轴相交于点A,与y轴相交于点B,AB=2![]() .点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
.点P在抛物线上,线段AP与y轴的正半轴交于点C,线段BP与x轴相交于点D,设点P的横坐标为m.
(1)求这条抛物线的解析式;
(2)用含m的代数式表示线段CO的长;
(3)当tan∠ODC=![]() 时,求∠PAD的正弦值.
时,求∠PAD的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的图像经过点(0,1),且当x=2时,函数有最大值为4,
(1)求函数表达式
(2)直接写出:当x取何值时,函数值大于1
(3)写出将函数图像向左平移1个单位,向上平移2个单位后所得到的函数表达式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com